题目内容

15．给出一个算法：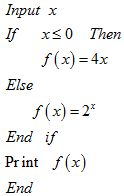

根据以上算法，可求得f（-1）+f（3）的值为4．

分析 根据算法语句写出分段函数，再根据分段函数求出相应的函数值即可．

解答 解：根据算法语句知，该程序运行后输出
函数f（x）=$\left\{\begin{array}{l}{4x，x≤0}\\{{2}^{x}，x＞0}\end{array}\right.$，
所以f（-1）+f（3）=4×（-1）+23=4．
故答案为：4．

点评 本题主要考查了利用条件语句表示分段函数的应用问题，是基础题目．

练习册系列答案
相关题目
5．在△ABC中，2AB=3AC，∠A=$\frac{π}{3}$，∠BAC的平分线交边BC于点D，|AD|=1，则（　　）
A．AB•AC=$\sqrt{2}$AB+ACB．AB+AC=$\sqrt{2}$AB•ACC．AB•AC=$\sqrt{3}$AB+ACD．AB+AC=$\sqrt{3}$AB•AC
6．下列有关命题的说法正确的是（　　）
A．命题“若x2=1，则x=1”的否命题为：“若x2=1，则x≠1”
B．“x=-1”是“x2-5x-6=0”的必要不充分条件
C．命题“?x∈R，使得x2+x+1＜0”的否定是：“?x∈R，均有x2+x+1＜0”
D．命题“若x＞1，则$\frac{1}{x}$＜1”的逆否命题为真命题
3．直线l：y=kx+1与双曲线C：2x2-y2=1．
（1）若直线与双曲线有且仅有一个公共点，求实数k的取值范围；
（2）若直线分别与双曲线的两支各有一个公共点，求实数k的取值范围．
10．一个袋中装有大小相同的5个白球和3个红球，现在不放回的取2次球，每次取出一个球，记“第1次拿出的是白球”为事件A，“第2次拿出的是白球”为事件B，则P（B|A）是（　　）
A．$\frac{5}{8}$B．$\frac{5}{16}$C．$\frac{4}{7}$D．$\frac{5}{14}$
20．已知数列{an}，a1=1，an+1=an+2n，计算数列{an}的第100项．现已给出该问题算法的流程图（如图1所示）

（1）请在图1中判断框的A、B、C（其中A中用i的关系表示）处填上合适的语句，使之完成该问题的算法功能．
（2）根据流程图1补充完整程序语言（如图2）（即在D、E、F处填写合适的语句）．
解：（将答案写在下面相应位置）
7．已知函数f（x）=ex-kx+k（k∈R）．
（1）试讨论函数y=f（x）的单调性；
（2）若该函数有两个不同的零点x1，x2试求实数k取值范围．
4．已知f（x）是定义在R上的奇函数，对任意x＞0，都有f（x+4）=f（x），若f（-2）=2，则f（2 018）等于（　　）
A．2 012B．2C．2 013D．-2
5．给出下列四个命题：
①两个向量相等，则它们的起点相同，终点相同；
②若$\overrightarrow{a}$=$\overrightarrow{b}$，$\overrightarrow{b}$=$\overrightarrow{c}$，则$\overrightarrow{a}$=$\overrightarrow{c}$；
③设$\overrightarrow{{a}_{0}}$是单位向量，若$\overrightarrow{d}$∥$\overrightarrow{{a}_{0}}$，且|$\overrightarrow{d}$|=1，则$\overrightarrow{d}$=$\overrightarrow{{a}_{0}}$；
④$\overrightarrow{d}$=$\overrightarrow{b}$的充要条件是|$\overrightarrow{d}$=|$\overrightarrow{b}$|且$\overrightarrow{d}$∥$\overrightarrow{b}$．
其中假命题的个数为（　　）
A．1B．2C．3D．4

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网