题目内容
2．在△ABC中，三个内角A，B，C的对边分别是a，b，c，若a=3，b=4，sinC=$\frac{1}{2}$，则此三角形的面积是（ ）| A． | 8 | B． | 6 | C． | 4 | D． | 3 |
分析 根据三角形的面积公式S△=$\frac{1}{2}$absinC，代入计算即可．
解答 解：△ABC中，a=3，b=4，sinC=$\frac{1}{2}$，
则此三角形的面积为
S△ABC=$\frac{1}{2}$absinC=$\frac{1}{2}$×3×4×$\frac{1}{2}$=3．
故选：D．
点评 本题考查了三角形的面积计算问题，是基础题目．
练习册系列答案
阅读快车系列答案
相关题目
12．若$α∈（0，\frac{π}{2}）$，若$cos（α+\frac{π}{6}）=\frac{4}{5}$，则$sin（2α+\frac{π}{3}）$的值为（ ）
| A． | $\frac{12}{25}$ | B． | $\frac{24}{25}$ | C． | $-\frac{24}{25}$ | D． | $-\frac{12}{25}$ |
10．一个袋中装有大小相同的5个白球和3个红球，现在不放回的取2次球，每次取出一个球，记“第1次拿出的是白球”为事件A，“第2次拿出的是白球”为事件B，则P（B|A）是（ ）
| A． | $\frac{5}{8}$ | B． | $\frac{5}{16}$ | C． | $\frac{4}{7}$ | D． | $\frac{5}{14}$ |
14．函数f（x）=（m2-m-1）xm是幂函数，且在x∈（0，+∞）上为增函数，则实数m的值是（ ）
| A． | -1 | B． | 2 | C． | 3 | D． | -1或2 |
11．
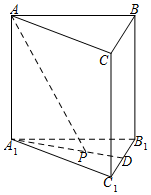已知正三棱柱（底面是正三角形，且侧棱与底面垂直的棱柱）ABC-A1B1C1体积为$\frac{9}{4}$，底面边长为$\sqrt{3}$．若P为底面A1B1C1的中心，则PA与平面ABC所成角的大小为（ ）
已知正三棱柱（底面是正三角形，且侧棱与底面垂直的棱柱）ABC-A1B1C1体积为$\frac{9}{4}$，底面边长为$\sqrt{3}$．若P为底面A1B1C1的中心，则PA与平面ABC所成角的大小为（ ）| A． | $\frac{π}{2}$ | B． | $\frac{π}{3}$ | C． | $\frac{π}{4}$ | D． | $\frac{π}{6}$ |
12．函数f（x）的定义域为R+，且对于任何正实数x、y都有f（xy）=f（x）+f（y），若f（8）=6，则f（$\sqrt{2}$）=（ ）
| A． | 1 | B． | 2 | C． | -1 | D． | $\sqrt{2}$ |