题目内容

17．在等差数列{an}中，an＞0，且a1+a2+…+a10=30，则a5+a6的值（　　）
A．3B．6C．9D．12

分析 由已知结合等差数列的性质可得5（a5+a6）=30，则答案可求．

解答 解：在等差数列{an}中，由an＞0，且a1+a2+…+a10=30，
得（a1+a10）+（a2+a9）+（a3+a8）+（a4+a7）+（a5+a6）=30，
即5（a5+a6）=30，∴a5+a6=6．
故选：B．

点评 本题考查等差数列的性质，是基础的计算题．

练习册系列答案
相关题目
7．已知函数f（x）=ex-kx+k（k∈R）．
（1）试讨论函数y=f（x）的单调性；
（2）若该函数有两个不同的零点x1，x2试求实数k取值范围．
8．圆x2+（y+1）2=3绕直线kx-y-1=0旋转一周所得的几何体的表面积为12π．
5．给出下列四个命题：
①两个向量相等，则它们的起点相同，终点相同；
②若$\overrightarrow{a}$=$\overrightarrow{b}$，$\overrightarrow{b}$=$\overrightarrow{c}$，则$\overrightarrow{a}$=$\overrightarrow{c}$；
③设$\overrightarrow{{a}_{0}}$是单位向量，若$\overrightarrow{d}$∥$\overrightarrow{{a}_{0}}$，且|$\overrightarrow{d}$|=1，则$\overrightarrow{d}$=$\overrightarrow{{a}_{0}}$；
④$\overrightarrow{d}$=$\overrightarrow{b}$的充要条件是|$\overrightarrow{d}$=|$\overrightarrow{b}$|且$\overrightarrow{d}$∥$\overrightarrow{b}$．
其中假命题的个数为（　　）
A．1B．2C．3D．4
12．函数f（x）的定义域为R+，且对于任何正实数x、y都有f（xy）=f（x）+f（y），若f（8）=6，则f（$\sqrt{2}$）=（　　）
A．1B．2C．-1D．$\sqrt{2}$
2．已知正三棱锥P-ABC，点P，A，B，C都在半径为$\sqrt{2}$的球面上，若PA，PB，PC两两相互垂直，则球心到截面ABC的距离为$\frac{\sqrt{2}}{3}$．
9．已知曲线 f（x）=ax2-2在横坐标为1的点 p处切线的倾斜角为$\frac{π}{4}$，则a=（　　）
A．$\frac{1}{2}$B．1C．2D．-1
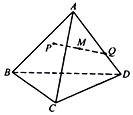6．如图，在三棱锥A-BCD中，AB⊥AD，AC⊥AD，∠BAC=60°，AB=AC=AD=4，点P，Q分别在侧面ABC棱AD上运动，PQ=2，M为线段PQ中点，当P，Q运动时，点M的轨迹把三棱锥A-BCD分成上、下两部分的体积之比等于$\frac{π}{{48\sqrt{3}-π}}$．
20．已知椭圆C：$\frac{{x}^{2}}{6}$+$\frac{{y}^{2}}{9}$=1，若P（x，y）是椭圆C上一动点，则x2+y2-2x的取值范围是（　　）
A．[6-2$\sqrt{6}$，9]B．[6-2$\sqrt{6}$，11]C．[6+2$\sqrt{6}$，9]D．[6+2$\sqrt{6}$，11]

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网