题目内容

16．已知a＞b＞0，则方程a2x2+b2y2=1与ax+by2=0的曲线在同一坐标系中大致是（　　）
A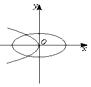．B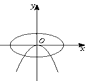．C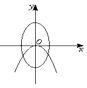．D．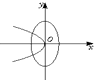

分析 根据题意，a＞b＞0，可以整理椭圆a2x2+b2y2=1与抛物线ax+by2=0变形为标准形式，可以判断其焦点所在的位置，进而分析选项可得答案．

解答 解：由a＞b＞0，
椭圆a2x2+b2y2=1，即$\frac{{x}^{2}}{\frac{1}{{a}^{2}}}+\frac{{y}^{2}}{\frac{1}{{b}^{2}}}$=1，焦点在y轴上；
抛物线ax+by2=0，即y2=-$\frac{a}{b}$x，焦点在x轴的负半轴上；
分析可得，D符合，
故选D．

点评 本题考查由椭圆、抛物线的方程判断图象的方法，注意先判断曲线的形状，再分析焦点等位置．

练习册系列答案
相关题目
6．下列有关命题的说法正确的是（　　）
A．命题“若x2=1，则x=1”的否命题为：“若x2=1，则x≠1”
B．“x=-1”是“x2-5x-6=0”的必要不充分条件
C．命题“?x∈R，使得x2+x+1＜0”的否定是：“?x∈R，均有x2+x+1＜0”
D．命题“若x＞1，则$\frac{1}{x}$＜1”的逆否命题为真命题
7．已知函数f（x）=ex-kx+k（k∈R）．
（1）试讨论函数y=f（x）的单调性；
（2）若该函数有两个不同的零点x1，x2试求实数k取值范围．
4．已知f（x）是定义在R上的奇函数，对任意x＞0，都有f（x+4）=f（x），若f（-2）=2，则f（2 018）等于（　　）
A．2 012B．2C．2 013D．-2
11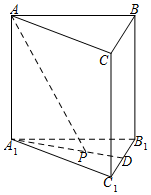．已知正三棱柱（底面是正三角形，且侧棱与底面垂直的棱柱）ABC-A1B1C1体积为$\frac{9}{4}$，底面边长为$\sqrt{3}$．若P为底面A1B1C1的中心，则PA与平面ABC所成角的大小为（　　）
A．$\frac{π}{2}$B．$\frac{π}{3}$C．$\frac{π}{4}$D．$\frac{π}{6}$
1．在平面直角坐标系xoy中，已知圆C1：x2+y2+6x-2y+6=0和圆C2：x2+y2-8x-10y+37=0若直线l过点A（4，0），且被圆C1截得的弦长为2$\sqrt{3}$，
（1）求直线l的方程
（2）求圆C2上的点到直线l的最远距离．
8．圆x2+（y+1）2=3绕直线kx-y-1=0旋转一周所得的几何体的表面积为12π．
5．给出下列四个命题：
①两个向量相等，则它们的起点相同，终点相同；
②若$\overrightarrow{a}$=$\overrightarrow{b}$，$\overrightarrow{b}$=$\overrightarrow{c}$，则$\overrightarrow{a}$=$\overrightarrow{c}$；
③设$\overrightarrow{{a}_{0}}$是单位向量，若$\overrightarrow{d}$∥$\overrightarrow{{a}_{0}}$，且|$\overrightarrow{d}$|=1，则$\overrightarrow{d}$=$\overrightarrow{{a}_{0}}$；
④$\overrightarrow{d}$=$\overrightarrow{b}$的充要条件是|$\overrightarrow{d}$=|$\overrightarrow{b}$|且$\overrightarrow{d}$∥$\overrightarrow{b}$．
其中假命题的个数为（　　）
A．1B．2C．3D．4
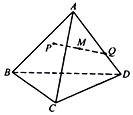6．如图，在三棱锥A-BCD中，AB⊥AD，AC⊥AD，∠BAC=60°，AB=AC=AD=4，点P，Q分别在侧面ABC棱AD上运动，PQ=2，M为线段PQ中点，当P，Q运动时，点M的轨迹把三棱锥A-BCD分成上、下两部分的体积之比等于$\frac{π}{{48\sqrt{3}-π}}$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网