题目内容
17.在△ABC中,D是BC中点,E是AB中点,CE交AD于点F,若$\overrightarrow{EF}=λ\overrightarrow{AB}+u\overrightarrow{AC}$,则λ+u=( )| A. | $-\frac{1}{6}$ | B. | $\frac{1}{6}$ | C. | $-\frac{1}{3}$ | D. | 1 |
分析 由于本题是选择题,不妨设△ABC为等边三角形,由题意可得F是△ABC的重心,即可得到$\overrightarrow{EF}$=$\frac{1}{3}$$\overrightarrow{EC}$=-$\frac{1}{6}$$\overrightarrow{AB}$+$\frac{1}{3}$$\overrightarrow{AC}$,继而求出λ,μ的值,问题得以解决.
解答 解:不妨设△ABC为等边三角形,D是BC中点,E是AB中点,CE交AD于点F,
∴F是△ABC的重心,
∴$\overrightarrow{EF}$=$\frac{1}{3}$$\overrightarrow{EC}$=$\frac{1}{3}$($\overrightarrow{EB}$+$\overrightarrow{BC}$)=$\frac{1}{3}$($\frac{1}{2}$$\overrightarrow{AB}$+$\overrightarrow{AC}$-$\overrightarrow{AB}$)=-$\frac{1}{6}$$\overrightarrow{AB}$+$\frac{1}{3}$$\overrightarrow{AC}$,
∵$\overrightarrow{EF}=λ\overrightarrow{AB}+u\overrightarrow{AC}$,
∴λ=-$\frac{1}{6}$,μ=$\frac{1}{3}$,
∴λ+μ=$\frac{1}{6}$,
故选:B.
点评 本题考查代数和的求法,是基础题,解题时要认真审题,注意平面向量的加法法则的合理运用

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
5.在△ABC中,2AB=3AC,∠A=$\frac{π}{3}$,∠BAC的平分线交边BC于点D,|AD|=1,则( )
| A. | AB•AC=$\sqrt{2}$AB+AC | B. | AB+AC=$\sqrt{2}$AB•AC | C. | AB•AC=$\sqrt{3}$AB+AC | D. | AB+AC=$\sqrt{3}$AB•AC |
12.若$α∈(0,\frac{π}{2})$,若$cos(α+\frac{π}{6})=\frac{4}{5}$,则$sin(2α+\frac{π}{3})$的值为( )
| A. | $\frac{12}{25}$ | B. | $\frac{24}{25}$ | C. | $-\frac{24}{25}$ | D. | $-\frac{12}{25}$ |
2.已知集合I,M,N的关系如图所示,则I,M,N的关系为( )
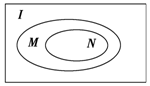

| A. | (∁IM)?(∁IN) | B. | M⊆(∁IN) | C. | (∁IM)⊆(∁IN) | D. | M?(∁IN) |
6.下列有关命题的说法正确的是( )
| A. | 命题“若x2=1,则x=1”的否命题为:“若x2=1,则x≠1” | |
| B. | “x=-1”是“x2-5x-6=0”的必要不充分条件 | |
| C. | 命题“?x∈R,使得x2+x+1<0”的否定是:“?x∈R,均有x2+x+1<0” | |
| D. | 命题“若x>1,则$\frac{1}{x}$<1”的逆否命题为真命题 |