题目内容

若对于任意实数m，关于x的方程log2（ax2+2x+1）-m=0恒有解，则实数a的取值范围是
 
．
考点：函数的零点与方程根的关系
专题：函数的性质及应用
分析：由已知中关于x的方程log2（ax2+2x+1）-m=0恒有解，可得函数f（x）=log2（ax2+2x+1）的值域为R，则函数g（x）=ax2+2x+1的值域A满足：（0，+∞）⊆A，结合一次函数和二次函数的图象和性质，可得答案．
解答： 解：∵关于x的方程log2（ax2+2x+1）-m=0恒有解，
则函数f（x）=log2（ax2+2x+1）的值域为R，
则函数g（x）=ax2+2x+1的值域A满足：（0，+∞）⊆A，
当a=0时，满足条件，
当a≠0时，
a＞0
△=4-4a≥0
，解得a∈（0，1]，
综上所述实数a的取值范围是[0，1]，
故答案为：[0，1]
点评：本题考查函数的恒成立问题，解题时要认真审题，仔细解答，注意对数函数的性质的灵活运用．
练习册系列答案
相关题目
已知函数f（x）=-x|x-a|+1（x∈R）．
（Ⅰ）当a=1时，求使f（x）=x成立的x的值；
（Ⅱ）当a∈（0，3），求函数y=f（x）在x∈[1，2]上的最大值；
（Ⅲ）对于给定的正数a，有一个最大的正数M（a），使x∈[0，M（a）]时，都有|f（x）|≤2，试求出这个正数M（a），并求它的取值范围．
下列命题中，
①命题“?x∈（0，2），x2+2x+2＜0”的否定是“?x∈（0，2），x2+2x+2＞0”；
②
x＞1
y＞2
是
x+y＞3
xy＞2
的充要条件；
③一个命题的逆命题为真，它的否命题也一定为真；
④“9＜k＜15”是“方程
x2
15-k
+
y2
k-9
=1表示椭圆”的充要条件．
⑤设P是以F1、F2为焦点的双曲线一点，且
PF 1
•
PF 2
=0，若△PF1F2的面积为9，则双曲线的虚轴长为6；
其中真命题的是
 
（将正确命题的序号填上）．
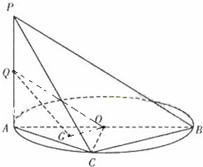如图，AB是⊙O的直径，PA垂直于⊙O所在的平面，C是圆上的点．
（1）求证：平面PAC⊥平面PBC．
（2）设Q为PA的中点，G为△AOC的重心，求证：OG∥平面PBC．
已知F1（-c，0），F2（c，0）是双曲线的左、右焦点．若P为双曲线右支上的一点，满足
PF1
•
PF2
=4ac，∠F1PF2=
π
3
，则该双曲线的离心率是
 
．
将棱长为2的正方形割除若干部分后的一几何体，其三视图如右图所示，则该几何体的体积等于
 
．
已知双曲线
x2
9-k
+
y2
k-4
=1的离心率e＜2，则k的取值范围是
 
．
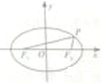如图，已知F1，F2是椭圆
x2
36
+
y2
24
=1的两个焦点，P为椭圆上一点，∠F1PF2=60°求：
（1）△PF1F2的面积；
（2）点P的坐标．
已知函数f（x）=sin（ωx+φ）（ω＞1，0≤φ≤π）是R上的偶函数，其图象关于M（
3π
4
，0）对称，且在区间[0，
π
2
]上是单调函数．
（1）求f（x）的解析式；
（2）求f（x）的单调递增区间；
（3）求函数y=
-f(x)-
1
2
的定义域．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网