Question

将棱长为2的正方形割除若干部分后的一几何体，其三视图如右图所示，则该几何体的体积等于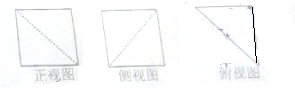

 

．

Answer 1

考点：由三视图求面积、体积

专题：空间位置关系与距离

分析：由于几何体的三视图中有两个正方形，一个三角形，由此得出该几何体是一个直三棱柱，去掉一个三棱锥，求出该几何体的体积即可．

解答： 解：根据几何体的三视图，得出该几何体是四棱锥，如图所示；
该几何体的体积是V_四棱锥=

1

3

•S_底面积•h
=

1

3

•2×

2

•

2

=

4

3

．
故答案为：

4

3

．

点评：本题考查了空间几何体的三视图的应用问题，解题时应根据三视图得出几何体是什么图形，是基础题．