Question

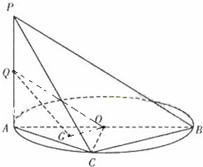如图，AB是⊙O的直径，PA垂直于⊙O所在的平面，C是圆上的点．
（1）求证：平面PAC⊥平面PBC．
（2）设Q为PA的中点，G为△AOC的重心，求证：OG∥平面PBC．

Answer 1

考点：平面与平面垂直的判定,直线与平面平行的判定

专题：空间位置关系与距离

分析：（1）根据面面垂直的判定定理即可证明平面PAC⊥平面PBC．
（2）根据面面平行的性质证明平面QOE∥平面PBC即可证明OG∥平面PBC．

解答： 证明：（1）∵AB是⊙O的直径，∴BC⊥AC，
∵PA垂直于⊙O所在的平面，BC?⊙O所在的平面，
∴PA⊥BC，
∵PA∩AC=A，
∴BC⊥平面PAC，
∵BC?平面PBC，
∴平面PAC⊥平面PBC．
（2）∵G为△AOC的重心，
∴延长OG交AC于E，则E是AC的中点，
连结QE，则QE是三角形PAC的中位线，
∴QE∥PC，
∵OQ是三角形PAB的中位线，
∴QO∥PA，
∵QE∩QO=Q，
∴平面QOE∥平面PBC，
∵OQ?平面QOE，
∴OG∥平面PBC．

点评：本题主要考查面面垂直的判定，以及面面平行的性质定理的应用，要求熟练掌握相应的判定定理和性质定理．