Question

9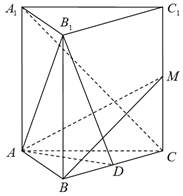．在正三棱柱ABC-A₁B₁C₁中，AA₁=2AB，点D是BC的中点，点M在CC₁上，且$CM=\frac{1}{8}C{C_1}$．
（1）求证：A₁C∥平面AB₁D；
（2）求证：平面AB₁D⊥平面ABM．

Answer 1

分析 如图以A为原点，以AC，AA₁为y、z轴建立空间直角坐标系．设AB=4，则AA₁=8，CM=1．则A（0，0，0），B（2$\sqrt{3}$，2，0），C（0，4，0）．
A₁（0，0，8），B₁（2$\sqrt{3}$，2，8），C₁（0，4，8），D（$\sqrt{3}$，3，0），M（0，4，1），利用向量法求解．

解答 解：如图以A为原点，以AC，AA₁为y、z轴建立空间直角坐标系．
设AB=4，则AA₁=8，CM=1．则A（0，0，0），B（2$\sqrt{3}$，2，0），C（0，4，0）．
A₁（0，0，8），B₁（2$\sqrt{3}$，2，8），C₁（0，4，8），D（$\sqrt{3}$，3，0），M（0，4，1）
（1）设面AB₁D的法向量为$\overrightarrow{m}=（x，y，z）$
$\overrightarrow{A{B}_{1}}=（2\sqrt{3}，2，8），\overrightarrow{AD}=（\sqrt{3}，3，0）$
由$\left\{\begin{array}{l}{\overrightarrow{m}•\overrightarrow{A{B}_{1}}=2\sqrt{3}x+2y+8z=0}\\{\overrightarrow{m}•\overrightarrow{AD}=\sqrt{3}x+3y=0}\end{array}\right.$
可取$\overrightarrow{m}=（\sqrt{3}，-1，-\frac{1}{2}）$
$\overrightarrow{{A}_{1}C}=（0，4，-8）$
，$\overrightarrow{{A}_{1}C}•\overrightarrow{m}=0-4+4=0$，则${A}_{1}C⊥\overrightarrow{m}$
∵A₁C?面AB₁D，∴A₁C∥平面AB₁D


（2）设面ABNM的法向量为$\overrightarrow{n}=（a，b，c）$
$\overrightarrow{AB}=（2\sqrt{3}，2，0）$，$\overrightarrow{AM}=（0，4，1）$
由$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{AB}=2\sqrt{3}x+2y=0}\\{\overrightarrow{n}•\overrightarrow{AM}=4y+z=0}\end{array}\right.$，可取$\overrightarrow{n}=（\sqrt{3}，-3，12）$
由（1）得面AB₁D的法向量为$\overrightarrow{m}=（\sqrt{3}，-1，-\frac{1}{2}）$，
$\overrightarrow{m}•\overrightarrow{n}$=$\sqrt{3}×\sqrt{3}$+（-1）×（-3）+12×$（-\frac{1}{2}）$=0
∴$\overrightarrow{m}⊥\overrightarrow{n}$，∴平面AB₁D⊥平面ABM

点评 本题考查了空间线面平行、面面垂直的判定，熟练掌握向量法的应用是解题的关键，属于中档题．