题目内容
19.若函数f(x)=sin(ωx)(ω>0)在$[{\frac{π}{4},\frac{π}{2}}]$上为减函数,则ω的取值范围为( )| A. | (0,3] | B. | (0,4] | C. | [2,3] | D. | [2,+∞) |
分析 由题意利用正弦函数的单调性可得,ω•$\frac{π}{4}$≥2kπ+$\frac{π}{2}$,且ω•$\frac{π}{2}$≤2kπ+$\frac{3π}{2}$,k∈Z,由此求得ω的取值范围.
解答 解:∵函数f(x)=sin(ωx)(ω>0)在$[{\frac{π}{4},\frac{π}{2}}]$上为减函数,∴ω•$\frac{π}{4}$≥2kπ+$\frac{π}{2}$,且ω•$\frac{π}{2}$≤2kπ+$\frac{3π}{2}$,k∈Z,
求得8k+2≤ω≤4k+3.
令k=0,求得2≤ω≤3,
故选:C.
点评 本题主要考查正弦函数的单调性,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.已知函数f(x)=$\left\{\begin{array}{l}{\frac{1}{2}-|x-\frac{3}{2}|(x≤2)}\\{{e}^{x-2}(-{x}^{2}+8x-12)(x>2)}\end{array}\right.$,若在区间(1,∞)上存在n(n≥2)个不同的数x1,x2,x3,…,xn,使得$\frac{f({x}_{1})}{{x}_{1}}$=$\frac{f({x}_{2})}{{x}_{2}}$=…$\frac{f({x}_{n})}{{x}_{n}}$成立,则n的取值集合是( )
| A. | {2,3,4,5} | B. | {2,3} | C. | {2,3,5} | D. | {2,3,4} |
14.已知集合A={x|-1<x<2},B={x|0<x<2},则∁AB=( )
| A. | (-1,0) | B. | (-1,0] | C. | (0,2) | D. | [0,2) |
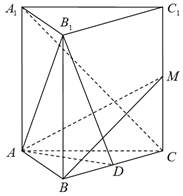 在正三棱柱ABC-A1B1C1中,AA1=2AB,点D是BC的中点,点M在CC1上,且$CM=\frac{1}{8}C{C_1}$.
在正三棱柱ABC-A1B1C1中,AA1=2AB,点D是BC的中点,点M在CC1上,且$CM=\frac{1}{8}C{C_1}$.