题目内容
14.若实数x,y,z满足4x+3y+12z=1,求x2+y2+z2的最小值.分析 利用条件x+2y+3z=1,构造柯西不等式(4x+3y+12z)2≤(x2+y2+z2)(42+32+122),变形即可得答案.
解答 解:根据题意,实数x,y,z满足4x+3y+12z=1,
则有(4x+3y+12z)2≤(x2+y2+z2)(42+32+122),
即1≤169(x2+y2+z2),
即有x2+y2+z2≥$\frac{1}{169}$;
即x2+y2+z2的最小值为$\frac{1}{169}$;
故答案为:$\frac{1}{169}$.
点评 本题考查柯西不等式的应用,关键是熟练掌握柯西不等式的形式及变形应用.

练习册系列答案
相关题目
4.已知实数x,y满足$\left\{{\begin{array}{l}{x-y-1≥0}\\{x+y-3≥0}\\{y≤3}\end{array}}\right.$则2x+y的最小值为( )
| A. | 11 | B. | 3 | C. | 4 | D. | 2 |
6.已知向量$\overrightarrow{a}$=(-1,2),b=(0,3),如果向量$\overrightarrow{a}$+2$\overrightarrow{b}$与$\overrightarrow{a}$-x$\overrightarrow{b}$垂直,则实数x的值为( )
| A. | 1 | B. | -1 | C. | $\frac{17}{24}$ | D. | -$\frac{17}{24}$ |
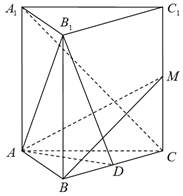 在正三棱柱ABC-A1B1C1中,AA1=2AB,点D是BC的中点,点M在CC1上,且$CM=\frac{1}{8}C{C_1}$.
在正三棱柱ABC-A1B1C1中,AA1=2AB,点D是BC的中点,点M在CC1上,且$CM=\frac{1}{8}C{C_1}$.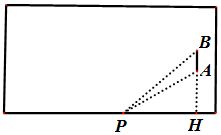 如图所示的矩形是长为100码,宽为80码的足球比赛场地.其中PH是足球场地边线所在的直线,AB是球门,且AB=8码.从理论研究及经验表明:当足球运动员带球沿着边线奔跑时,当运动员(运动员看做点P)所对AB的张角越大时,踢球进球的可能性就越大.
如图所示的矩形是长为100码,宽为80码的足球比赛场地.其中PH是足球场地边线所在的直线,AB是球门,且AB=8码.从理论研究及经验表明:当足球运动员带球沿着边线奔跑时,当运动员(运动员看做点P)所对AB的张角越大时,踢球进球的可能性就越大.