题目内容
4.公差不为零的等差数列{an}的前n项和为Sn,若a4是a2与a7的等比中项,S5=50,则S8等于104.分析 利用等差数列通项公式、前n项和公式和等比中项定义,列出方程组,求出a1=6,d=2,由此能求出S8.
解答 解:∵公差不为零的等差数列{an}的前n项和为Sn,
a4是a2与a7的等比中项,S5=50,
∴$\left\{\begin{array}{l}{({a}_{1}+3d)^{2}=({a}_{1}+d)({a}_{1}+6d)}\\{5{a}_{1}+\frac{5×4}{2}d=50}\\{d≠0}\end{array}\right.$,
解得a1=6,d=2,
∴S8=$8×6+\frac{8×7}{2}×2$=104.
故答案为:104.
点评 本题考查等差数列的前8项和的求法,考查等差数列、等比中项等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想,函数与方程思想,是基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
14.已知集合A={x|-1<x<2},B={x|0<x<2},则∁AB=( )
| A. | (-1,0) | B. | (-1,0] | C. | (0,2) | D. | [0,2) |
12.将函数f(x)=cos2x图象向左平移φ(0<φ<$\frac{π}{2}$)个单位后得到函数g(x)的图象,若函数g(x)在区间[-$\frac{π}{6}$,$\frac{π}{6}$]上单调递减,且函数g(x)的最大负零点在区间(-$\frac{π}{6}$,0)上,则φ的取值范围是( )
| A. | [$\frac{π}{12}$,$\frac{π}{4}$] | B. | [$\frac{π}{3}$,$\frac{5π}{12}$) | C. | ($\frac{π}{4}$,$\frac{π}{3}$] | D. | [$\frac{π}{6}$,$\frac{π}{4}$) |
19.某校为了解800名高一新生的身体生长状况,用系统抽样法(按等距的规则)抽取50名同学进行检查,将学生从1~800进行编号,现已知第17组抽取的号码为263,则第一组用简单随机抽样抽取的号码为7.
16.设i为虚数单位,n为正整数,θ∈[0,2π).
(1)用数学归纳法证明:(cosθ+isinθ)n=cosnθ+isinnθ;
(2)已知$z=\sqrt{3}-i$,试利用(1)的结论计算z10.
(1)用数学归纳法证明:(cosθ+isinθ)n=cosnθ+isinnθ;
(2)已知$z=\sqrt{3}-i$,试利用(1)的结论计算z10.
14.已知函数满足一下两个条件:①任意x1,x2∈(0,+∞),且x1≠x2时,(x1-x2)[f(x1)-f(x2)]<0;②对定义域内任意x有f(x)+f(-x)=0,则符合条件的函数是( )
| A. | f(x)=2x | B. | f(x)=1-|x| | C. | $f(x)=\frac{1}{x}-x$ | D. | f(x)=ln(x+1) |
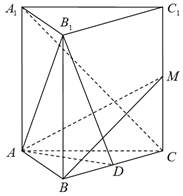 在正三棱柱ABC-A1B1C1中,AA1=2AB,点D是BC的中点,点M在CC1上,且$CM=\frac{1}{8}C{C_1}$.
在正三棱柱ABC-A1B1C1中,AA1=2AB,点D是BC的中点,点M在CC1上,且$CM=\frac{1}{8}C{C_1}$.