题目内容
18.已知集合A={x|0<x≤1},B={x|x2<1},则(∁RA)∩B=( )| A. | (0,1) | B. | [0,1] | C. | (-1,1] | D. | (-1,0] |
分析 解关于B的不等式,求出A的补集,从而求出其和B的交集即可.
解答 解:∵集合A={x|0<x≤1},
∴∁RA=(-∞,0]∪(1,+∞),
∵B={x|x2<1}=(-1,1).
∴(∁RA)∩B=(-1,0]
故选:D.
点评 本题考查了集合的运算,考查补集以及交集问题,是一道基础题.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
6.已知向量$\overrightarrow{a}$=(-1,2),b=(0,3),如果向量$\overrightarrow{a}$+2$\overrightarrow{b}$与$\overrightarrow{a}$-x$\overrightarrow{b}$垂直,则实数x的值为( )
| A. | 1 | B. | -1 | C. | $\frac{17}{24}$ | D. | -$\frac{17}{24}$ |
10.在直四棱柱ABCD-A1B1C1D1中,底面ABCD为菱形,E,F分别是BB1,DD1的中点,G为AE的中点且FG=3,则△EFG的面积的最大值为( )
| A. | $\frac{3}{2}$ | B. | 3 | C. | $2\sqrt{3}$ | D. | $\frac{{9\sqrt{3}}}{4}$ |
7.已知函数$f(x)=sin2ωx-2\sqrt{3}{cos^2}ωx+1(ω>0)$在区间(π,2π)内没有极值点,则ω的取值范围为( )
| A. | $({\frac{5}{12},\frac{11}{24}}]$ | B. | $({0,\frac{5}{12}}]∪[{\frac{11}{24},\frac{1}{2}})$ | C. | $({0,\frac{1}{2}})$ | D. | $({0,\frac{5}{24}}]∪[{\frac{5}{12},\frac{11}{24}}]$ |
7.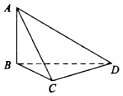 在我国古代数学名著《九章算术》中,将四个面都为直角三角形的四面体称为鳖臑,如图,在鳖臑ABCD中,AB⊥平面BCD,且AB=BC=CD,则异面直线AC与BD所成角的余弦值为( )
在我国古代数学名著《九章算术》中,将四个面都为直角三角形的四面体称为鳖臑,如图,在鳖臑ABCD中,AB⊥平面BCD,且AB=BC=CD,则异面直线AC与BD所成角的余弦值为( )
 在我国古代数学名著《九章算术》中,将四个面都为直角三角形的四面体称为鳖臑,如图,在鳖臑ABCD中,AB⊥平面BCD,且AB=BC=CD,则异面直线AC与BD所成角的余弦值为( )
在我国古代数学名著《九章算术》中,将四个面都为直角三角形的四面体称为鳖臑,如图,在鳖臑ABCD中,AB⊥平面BCD,且AB=BC=CD,则异面直线AC与BD所成角的余弦值为( )| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | -$\frac{\sqrt{3}}{2}$ |
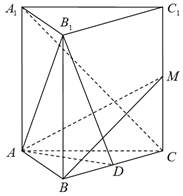 在正三棱柱ABC-A1B1C1中,AA1=2AB,点D是BC的中点,点M在CC1上,且$CM=\frac{1}{8}C{C_1}$.
在正三棱柱ABC-A1B1C1中,AA1=2AB,点D是BC的中点,点M在CC1上,且$CM=\frac{1}{8}C{C_1}$.