题目内容
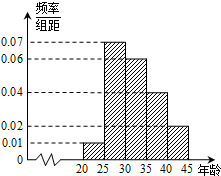 某市为增强市民的环境保护意识,面向全市征召义务宣传志愿者,现从符合条件的志愿者中随机抽取100名,按年龄所在的区间分组:第1组:[20,25);第2组:[25,30);第3组:[30,35);第4组:[35,40);第5组:[40,45].得到的频率分布直方图如下图所示.
某市为增强市民的环境保护意识,面向全市征召义务宣传志愿者,现从符合条件的志愿者中随机抽取100名,按年龄所在的区间分组:第1组:[20,25);第2组:[25,30);第3组:[30,35);第4组:[35,40);第5组:[40,45].得到的频率分布直方图如下图所示.(1)若从第3,4,5组中用分层抽样的方法抽取6名志愿者参加广场的宣传活动,应从第3,4,5组各抽取多少名志愿者?
(2)在满足条件(1)时,该市决定在这6名志愿者中随机抽取2名志愿者介绍宣传经验,求第4组至少有一名志愿者被抽中的概率.
考点:频率分布直方图
专题:概率与统计
分析:(1)根据频率=
,求出第3、4、5组的人数,再计算用分层抽样方法在各组应抽取的人数;
(2)利用列举法求出从6名志愿者中取2名志愿者的基本事件数以及第4组的2名志愿者至少有一名被抽中的基本事件数,求出对应的概率即可.
| 频数 |
| 样本容量 |
(2)利用列举法求出从6名志愿者中取2名志愿者的基本事件数以及第4组的2名志愿者至少有一名被抽中的基本事件数,求出对应的概率即可.
解答:
解:(1)第3组的人数为0.06×5×100=30,
第4组的人数为0.04×5×100=20,
第5组的人数为0.02×5×100=10,
所以第3,4,5组共60名志愿者;
利用分层抽样的方法在60名志愿者中抽取6名志愿者,每组抽取的人数为:
第3组:
=3,
第4组:
=2,
第5组:
=1;
所以应从第3,4,5组中分别抽取的人数为3人,2人,1人;
(2)记第3组的3名志愿者为A1,A2,A3,第4组的2名志愿者为B1,B2,
第5组的1名志愿者为C1;
从6名志愿者中取2名志愿者有:
(A1,A2),(A1,A3)(A1,B1),(A1,B2),(A1,C1),
(A2,A3),(A2,B1),(A2,B2),(A2,C1),
(A3,B1),(A3,B2),(A3,C1),
(B1,B2),(B1,C1),(B2,C1)共15种方法;
其中第4组的2名志愿者B1,B2至少有一名志愿者被抽中的有:
(A1,B1),(A1,B2),(A2,B1),(A2,B2),(A3,B1),
(A3,B2),(B1,B2),(B1,C1),(B2,C1)共9种;
所以第4组至少有一名志愿者被抽中的概率为
=
.
第4组的人数为0.04×5×100=20,
第5组的人数为0.02×5×100=10,
所以第3,4,5组共60名志愿者;
利用分层抽样的方法在60名志愿者中抽取6名志愿者,每组抽取的人数为:
第3组:
| 30×6 |
| 60 |
第4组:
| 20×6 |
| 60 |
第5组:
| 10×6 |
| 60 |
所以应从第3,4,5组中分别抽取的人数为3人,2人,1人;
(2)记第3组的3名志愿者为A1,A2,A3,第4组的2名志愿者为B1,B2,
第5组的1名志愿者为C1;
从6名志愿者中取2名志愿者有:
(A1,A2),(A1,A3)(A1,B1),(A1,B2),(A1,C1),
(A2,A3),(A2,B1),(A2,B2),(A2,C1),
(A3,B1),(A3,B2),(A3,C1),
(B1,B2),(B1,C1),(B2,C1)共15种方法;
其中第4组的2名志愿者B1,B2至少有一名志愿者被抽中的有:
(A1,B1),(A1,B2),(A2,B1),(A2,B2),(A3,B1),
(A3,B2),(B1,B2),(B1,C1),(B2,C1)共9种;
所以第4组至少有一名志愿者被抽中的概率为
| 9 |
| 15 |
| 3 |
| 5 |
点评:本题考查了频率、频数与样本容量的应用问题,也考查了用列举法求古典概型的概率问题,是基础题目.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
从3名语文老师、4名数学老师和5名英语老师中选派5人组成一个支教小组,则语文、数学和英语老师都至少有1人的选派方法种数是( )
| A、590 | B、570 |
| C、360 | D、210 |
函数y=ecosx(-π≤x≤π)的大致图象为( )
A、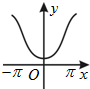 |
B、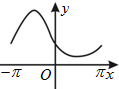 |
C、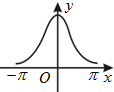 |
D、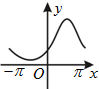 |
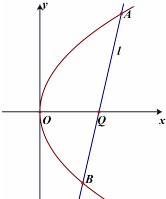 已知抛物线G:y2=2px(p>0)的焦点到准线的距离为2,过点Q(a,0)(a>0)的直线l交抛物线G于A,B两点(如图所示).
已知抛物线G:y2=2px(p>0)的焦点到准线的距离为2,过点Q(a,0)(a>0)的直线l交抛物线G于A,B两点(如图所示).