题目内容
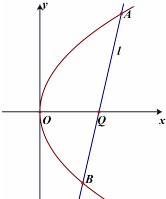 已知抛物线G:y2=2px(p>0)的焦点到准线的距离为2,过点Q(a,0)(a>0)的直线l交抛物线G于A,B两点(如图所示).
已知抛物线G:y2=2px(p>0)的焦点到准线的距离为2,过点Q(a,0)(a>0)的直线l交抛物线G于A,B两点(如图所示). (Ⅰ)求抛物线G的方程;
(Ⅱ)有人发现,当点Q为抛物线的焦点时,
| 1 |
| |QA| |
| 1 |
| |QB| |
| 1 |
| |QA|2 |
| 1 |
| |QB|2 |
考点:直线与圆锥曲线的综合问题,抛物线的标准方程,直线与圆锥曲线的关系
专题:圆锥曲线的定义、性质与方程
分析:(Ⅰ)利用抛物线G:y2=2px(p>0)中p的几何意义就是焦点到准线的距离,直接求解抛物线G的方程.(Ⅱ)解法一:直线l交抛物线G于A,B两点,设直线AB:x=my+a.联立方程组
,通过△>0,得到a>-m2时,直线l与抛物线G相交,设交点的坐标为A(x1,y1),B(x2,y2),利用韦达定理,弦长公式化简
+
,利用表达式是定值,推出当且仅当a=2时,式子(?)与m的取值无关,
得到存在唯一的一个点Q(2,0).
解法二:直线AB的斜率k存在,设直线AB:y=k(x-a),联立方程组
,设交点的坐标为A(x1,y1),B(x2,y2),利用韦达定理以及弦长公式,表示
+
是定值,说明式子的值与k无关.
求得a得到定点定值即可.
|
| 1 |
| |QA|2 |
| 1 |
| |QB|2 |
得到存在唯一的一个点Q(2,0).
解法二:直线AB的斜率k存在,设直线AB:y=k(x-a),联立方程组
|
| 1 |
| |QA|2 |
| 1 |
| |QB|2 |
求得a得到定点定值即可.
解答:
解:(Ⅰ)因为抛物线G:y2=2px(p>0)中p的几何意义就是焦点到准线的距离,
所以抛物线G的方程是y2=4x.
(Ⅱ)解法一:
因为直线l交抛物线G于A,B两点,所以直线AB的斜率必不为0.
设直线AB:x=my+a.
联立方程组
得y2-4my-4a=0.
当△=16m2+16a>0,即a>-m2时,直线l与抛物线G相交,
设交点的坐标为A(x1,y1),B(x2,y2),则y1+y2=4m,y1y2=-4a.
所以|QA|=
=
|y1|,同理可得|QB|=
|y2|,
所以
+
=
(
+
)=
•
=
•
=
•
=
•
.(?)
若
+
是定值,则式子(?)与m的取值无关.
因为当且仅当a=2时,式子(?)与m的取值无关,
所以存在唯一的一个点Q(2,0),使得
+
的值也与直线l的方向无关(此时,
+
恒为定值
).
解法二:
由条件可知直线AB的斜率不为0,
若直线AB的斜率k存在,设直线AB:y=k(x-a),
联立方程组
得k2x2-(2k2a+4)x+k2a2=0,
当△=(2k2a+4)2-4k4a2=16k2a+16>0时,直线l与抛物线G相交.
设交点的坐标为A(x1,y1),B(x2,y2),则x1+x2=
,x1x2=a2.
所以|QA|=
=
|x1-a|,同理可得|QB|=
|x2-a|,
所以
+
=
(
+
)=
•
=
•
(?)
若
+
是定值,则式子(?)的值与k无关.
因为当且仅当8a=16,a=2时,式子(?)的值与k无关,
所以存在点Q(2,0),使得
+
恒为定值
.
若直线AB斜率不存在,即直线AB:x=2,
此时|QA|2=|QB|2=8,也满足
+
=
.
综上可知,能找到一个点Q,使得
+
的值也与直线l的方向无关(如取Q(2,0),则
+
恒为定值
).
所以抛物线G的方程是y2=4x.
(Ⅱ)解法一:
因为直线l交抛物线G于A,B两点,所以直线AB的斜率必不为0.
设直线AB:x=my+a.
联立方程组
|
当△=16m2+16a>0,即a>-m2时,直线l与抛物线G相交,
设交点的坐标为A(x1,y1),B(x2,y2),则y1+y2=4m,y1y2=-4a.
所以|QA|=
(x1-a)2+
|
| m2+1 |
| m2+1 |
所以
| 1 |
| |QA|2 |
| 1 |
| |QB|2 |
| 1 |
| m2+1 |
| 1 |
| y12 |
| 1 |
| y22 |
| 1 |
| m2+1 |
| y12+y22 |
| (y1y2)2 |
| 1 |
| m2+1 |
| (y1+y2)2-2y1y2 |
| (y1y2)2 |
| 1 |
| m2+1 |
| 16m2+8a |
| 16a2 |
| 1 |
| m2+1 |
m2+
| ||
| a2 |
若
| 1 |
| |QA|2 |
| 1 |
| |QB|2 |
因为当且仅当a=2时,式子(?)与m的取值无关,
所以存在唯一的一个点Q(2,0),使得
| 1 |
| |QA|2 |
| 1 |
| |QB|2 |
| 1 |
| |QA|2 |
| 1 |
| |QB|2 |
| 1 |
| 4 |
解法二:
由条件可知直线AB的斜率不为0,
若直线AB的斜率k存在,设直线AB:y=k(x-a),
联立方程组
|
当△=(2k2a+4)2-4k4a2=16k2a+16>0时,直线l与抛物线G相交.
设交点的坐标为A(x1,y1),B(x2,y2),则x1+x2=
| 2k2a+4 |
| k2 |
所以|QA|=
(x1-a)2+
|
| k2+1 |
| k2+1 |
所以
| 1 |
| |QA|2 |
| 1 |
| |QB|2 |
| 1 |
| k2+1 |
| 1 |
| (x1-a)2 |
| 1 |
| (x2-a)2 |
| 1 |
| k2+1 |
| (x1-a)2+(x2-a)2 |
| (x1-a)2•(x2-a)2 |
| 1 |
| k2+1 |
| 8k2a+16 |
| 16a2 |
若
| 1 |
| |QA|2 |
| 1 |
| |QB|2 |
因为当且仅当8a=16,a=2时,式子(?)的值与k无关,
所以存在点Q(2,0),使得
| 1 |
| |QA|2 |
| 1 |
| |QB|2 |
| 1 |
| 4 |
若直线AB斜率不存在,即直线AB:x=2,
此时|QA|2=|QB|2=8,也满足
| 1 |
| |QA|2 |
| 1 |
| |QB|2 |
| 1 |
| 4 |
综上可知,能找到一个点Q,使得
| 1 |
| |QA|2 |
| 1 |
| |QB|2 |
| 1 |
| |QA|2 |
| 1 |
| |QB|2 |
| 1 |
| 4 |
点评:本小题主要考查直线、抛物线、直线与抛物线的位置关系等基础知识,考查推理论证能力、运算求解能力、抽象概括能力,考查化归与转化思想、分类与整合思想、函数与方程思想、数形结合思想等.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
已知椭圆C:
+
=1(a>b>0)的左、右焦点分别是F1,F2,右顶点为A,上顶点为B,若椭圆C的中点到直线AB的距离为
|F1F2|,则椭圆C的离心率e=( )
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 6 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
下列命题错误的是( )
A、“?x∈R,x+
| ||||
| B、命题“若一个数是负数,则它的平方是非负数”的否命题是假命题 | ||||
| C、函数f(x)=sin4x+cos4x的最小正周期为π | ||||
D、若关于x的方程x2+2px+1=0有实根,则方程(x2+px)
|
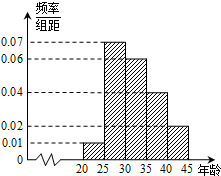 某市为增强市民的环境保护意识,面向全市征召义务宣传志愿者,现从符合条件的志愿者中随机抽取100名,按年龄所在的区间分组:第1组:[20,25);第2组:[25,30);第3组:[30,35);第4组:[35,40);第5组:[40,45].得到的频率分布直方图如下图所示.
某市为增强市民的环境保护意识,面向全市征召义务宣传志愿者,现从符合条件的志愿者中随机抽取100名,按年龄所在的区间分组:第1组:[20,25);第2组:[25,30);第3组:[30,35);第4组:[35,40);第5组:[40,45].得到的频率分布直方图如下图所示.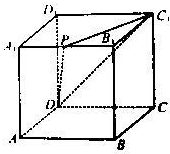 如图所示,若点P为正方体AC1的棱A1B1的中点,求截面PC1D和AA1B1B所成的锐二面角的余弦值.
如图所示,若点P为正方体AC1的棱A1B1的中点,求截面PC1D和AA1B1B所成的锐二面角的余弦值.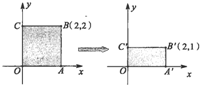 已知矩阵M=
已知矩阵M=