题目内容
从3名语文老师、4名数学老师和5名英语老师中选派5人组成一个支教小组,则语文、数学和英语老师都至少有1人的选派方法种数是( )
| A、590 | B、570 |
| C、360 | D、210 |
考点:计数原理的应用
专题:排列组合
分析:不同的组队方案:选派5人组成一个支教小组,要求其中语文、数学和英语老师都至少有1人,方法共有6类,他们分别是:3名语文、1名数学和1名英语;1名语文、3名数学和1名英语,…,在每一类中都用分步计数原理解答.
解答:
解:直接法:3名语文、1名数学和1名英语,有C33C41C51=20种,
1名语文、3名数学和1名英语1名,有C31C43C51=60种,
1名语文、1名数学和1名英语3名,有C31C41C53=120种,
2名语文、2名数学和1名英语1名,有C32C42C51=90种,
1名语文、2名数学和2名英语1名,有C31C42C52=180种,
2名语文、1名数学和2名英语1名,有C32C41C52=120种,
共计20+60+120+90+180+120=590种
故选:A.
1名语文、3名数学和1名英语1名,有C31C43C51=60种,
1名语文、1名数学和1名英语3名,有C31C41C53=120种,
2名语文、2名数学和1名英语1名,有C32C42C51=90种,
1名语文、2名数学和2名英语1名,有C31C42C52=180种,
2名语文、1名数学和2名英语1名,有C32C41C52=120种,
共计20+60+120+90+180+120=590种
故选:A.
点评:本题主要考查了排列、组合及简单计数问题,解答关键是利用直接法:先分类后分步.

练习册系列答案
相关题目
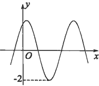 如图,函数f(x)=Asin(2x+φ)(A>0,|φ|<
如图,函数f(x)=Asin(2x+φ)(A>0,|φ|<| π |
| 2 |
| 3 |
A、(-
| ||
B、(-
| ||
C、(
| ||
D、(
|
已知函数y=f(x)是R上的减函数,且函数y=f(x-1)的图象关于点A(1,0)对称.设动点M(x,y),若实数x,y满足不等式 f(x2-8y+24)+f(y2-6x)≥0恒成立,则
•
的取值范围是( )
| OA |
| OM |
| A、(-∞,+∞) |
| B、[-1,1] |
| C、[2,4] |
| D、[3,5] |
数列{an}中,a1=1,a2n=n-an,a2n+1=an+1,则a100=( )
| A、30 | B、31 | C、32 | D、33 |
函数y=f(x)的图象如图所示,则函数f(x)有可能是( )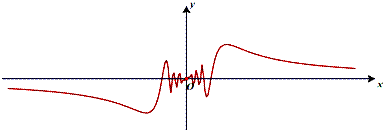

A、xsin(
| ||
B、xcos(
| ||
C、x2sin(
| ||
D、x2cos(
|
某程序框图如图所示,则输出的S的值为( )


| A、11 | B、19 | C、26 | D、57 |
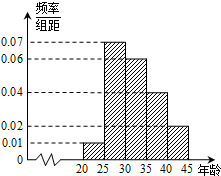 某市为增强市民的环境保护意识,面向全市征召义务宣传志愿者,现从符合条件的志愿者中随机抽取100名,按年龄所在的区间分组:第1组:[20,25);第2组:[25,30);第3组:[30,35);第4组:[35,40);第5组:[40,45].得到的频率分布直方图如下图所示.
某市为增强市民的环境保护意识,面向全市征召义务宣传志愿者,现从符合条件的志愿者中随机抽取100名,按年龄所在的区间分组:第1组:[20,25);第2组:[25,30);第3组:[30,35);第4组:[35,40);第5组:[40,45].得到的频率分布直方图如下图所示.