题目内容
定义在实数集R上的函数f(x),对任意x,y∈R,有f(x-y)+f(x+y)=2f(x)f(y),且f(0)≠0.
求证:f(x)是偶函数.
求证:f(x)是偶函数.
考点:抽象函数及其应用
专题:证明题,函数的性质及应用
分析:令x=y=0代入表达式,可得f(0)=1.再令x=0,y不变,即可获得f(-y)与f(y)之间的关系,从而获得函数的奇偶性.
解答:
证明:令x=y=0,则有f(0)+f(0)=2f(0)•f(0),
即2f(0)=2f(0)•f(0),
由于f(0)≠0,
即有f(0)=1.
令x=0,y=t,
则有f(t)+f(-t)=2f(0)f(t),
即有f(t)+f(-t)=2f(t),
即f(-t)=f(t),
即为f(-x)=f(x).
故y=f(x)是偶函数.
即2f(0)=2f(0)•f(0),
由于f(0)≠0,
即有f(0)=1.
令x=0,y=t,
则有f(t)+f(-t)=2f(0)f(t),
即有f(t)+f(-t)=2f(t),
即f(-t)=f(t),
即为f(-x)=f(x).
故y=f(x)是偶函数.
点评:本题考查的是抽象函数及其应用类问题.在解答的过程当中充分体现了抽象表达式的应用能力、特值的问题处理技巧以及必要的计算能力.同时函数的奇偶性定义也在题目中得到了体现.值得同学们体会和反思.

练习册系列答案
相关题目
已知椭圆C:
+
=1(a>b>0)的左、右焦点分别是F1,F2,右顶点为A,上顶点为B,若椭圆C的中点到直线AB的距离为
|F1F2|,则椭圆C的离心率e=( )
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 6 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
数列{an}中,a1=1,a2n=n-an,a2n+1=an+1,则a100=( )
| A、30 | B、31 | C、32 | D、33 |
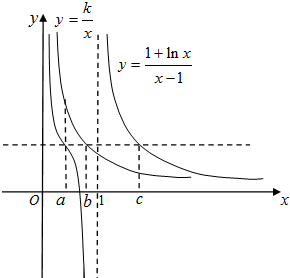 在平面直角坐标系xoy中,以O为极点,x轴的正半轴为极轴的极坐标系中,直线l的极坐标方程为θ=
在平面直角坐标系xoy中,以O为极点,x轴的正半轴为极轴的极坐标系中,直线l的极坐标方程为θ=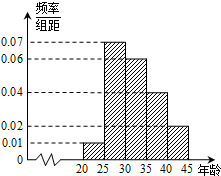 某市为增强市民的环境保护意识,面向全市征召义务宣传志愿者,现从符合条件的志愿者中随机抽取100名,按年龄所在的区间分组:第1组:[20,25);第2组:[25,30);第3组:[30,35);第4组:[35,40);第5组:[40,45].得到的频率分布直方图如下图所示.
某市为增强市民的环境保护意识,面向全市征召义务宣传志愿者,现从符合条件的志愿者中随机抽取100名,按年龄所在的区间分组:第1组:[20,25);第2组:[25,30);第3组:[30,35);第4组:[35,40);第5组:[40,45].得到的频率分布直方图如下图所示.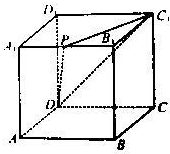 如图所示,若点P为正方体AC1的棱A1B1的中点,求截面PC1D和AA1B1B所成的锐二面角的余弦值.
如图所示,若点P为正方体AC1的棱A1B1的中点,求截面PC1D和AA1B1B所成的锐二面角的余弦值.