题目内容
已知a b c∈R+,a+
b+
c=2
,记a2+b2+c2的最小值为m.
(Ⅰ)求实数rn;
(Ⅱ)若关于x的不等式|x-3|≥m和x2+px+q≥0的解集相同,求p的值.
| 2 |
| 3 |
| 3 |
(Ⅰ)求实数rn;
(Ⅱ)若关于x的不等式|x-3|≥m和x2+px+q≥0的解集相同,求p的值.
考点:二维形式的柯西不等式,绝对值不等式的解法
专题:选作题,推理和证明
分析:(Ⅰ)由柯西不等式(a2+b2+c2)[12+(
)2+(
)2]≥(a+
b+
c)2=12,故a2+b2+c2≥2;
(Ⅱ)求出不等式|x-3|≥m的解集,利用韦达定理,即可求出p的值.
| 2 |
| 3 |
| 2 |
| 3 |
(Ⅱ)求出不等式|x-3|≥m的解集,利用韦达定理,即可求出p的值.
解答:
解:(Ⅰ)由柯西不等式(a2+b2+c2)[12+(
)2+(
)2]≥(a+
b+
c)2=12,
故a2+b2+c2≥2,
当且仅当
=
=
时取等号,
∴a2+b2+c2的最小值m为2;
(Ⅱ)不等式|x-3|≥m即不等式|x-3|≥2,解得x≥5或x≤1,
∴x2+px+q≥0的解集为{x|x≥5或x≤1},
∴p=-(1+5)=-6.
| 2 |
| 3 |
| 2 |
| 3 |
故a2+b2+c2≥2,
当且仅当
| a |
| 1 |
| b | ||
|
| c | ||
|
∴a2+b2+c2的最小值m为2;
(Ⅱ)不等式|x-3|≥m即不等式|x-3|≥2,解得x≥5或x≤1,
∴x2+px+q≥0的解集为{x|x≥5或x≤1},
∴p=-(1+5)=-6.
点评:本题考查绝对值不等式的解法,考查二维形式的柯西不等式,属于中档题.

练习册系列答案
相关题目
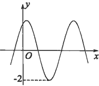 如图,函数f(x)=Asin(2x+φ)(A>0,|φ|<
如图,函数f(x)=Asin(2x+φ)(A>0,|φ|<| π |
| 2 |
| 3 |
A、(-
| ||
B、(-
| ||
C、(
| ||
D、(
|
在极坐标方程中,曲线C的方程是ρ=4sinθ,过点(4,
)作曲线C的切线,切线长为( )
| π |
| 6 |
| A、4 | ||
| B、7 | ||
C、2
| ||
| D、3 2 |
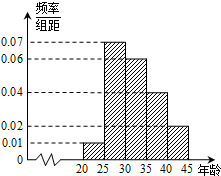 某市为增强市民的环境保护意识,面向全市征召义务宣传志愿者,现从符合条件的志愿者中随机抽取100名,按年龄所在的区间分组:第1组:[20,25);第2组:[25,30);第3组:[30,35);第4组:[35,40);第5组:[40,45].得到的频率分布直方图如下图所示.
某市为增强市民的环境保护意识,面向全市征召义务宣传志愿者,现从符合条件的志愿者中随机抽取100名,按年龄所在的区间分组:第1组:[20,25);第2组:[25,30);第3组:[30,35);第4组:[35,40);第5组:[40,45].得到的频率分布直方图如下图所示.