题目内容
已知f′(x0)=
,f(3)=2,f′(3)=-2,则
的值是( )
| lim |
| x→xo |
| f(x)-f(x0) |
| x-x0 |
| lim |
| x→3 |
| 2x-3f(x) |
| x-3 |
| A、4 | B、6 | C、8 | D、不存在 |
考点:极限及其运算
专题:导数的综合应用
分析:利用“罗比达法则”即可得出.
解答:
解:
=
(2-3f′(x))=2-3f′(3)=2-3×(-2)=8.
故选:C.
| lim |
| x→3 |
| 2x-3f(x) |
| x-3 |
| lim |
| x→3 |
故选:C.
点评:本题考查了“罗比达法则”,属于基础题.

练习册系列答案
相关题目
某程序框图如图所示,则输出的S的值为( )


| A、11 | B、19 | C、26 | D、57 |
下列命题错误的是( )
A、“?x∈R,x+
| ||||
| B、命题“若一个数是负数,则它的平方是非负数”的否命题是假命题 | ||||
| C、函数f(x)=sin4x+cos4x的最小正周期为π | ||||
D、若关于x的方程x2+2px+1=0有实根,则方程(x2+px)
|
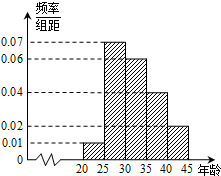 某市为增强市民的环境保护意识,面向全市征召义务宣传志愿者,现从符合条件的志愿者中随机抽取100名,按年龄所在的区间分组:第1组:[20,25);第2组:[25,30);第3组:[30,35);第4组:[35,40);第5组:[40,45].得到的频率分布直方图如下图所示.
某市为增强市民的环境保护意识,面向全市征召义务宣传志愿者,现从符合条件的志愿者中随机抽取100名,按年龄所在的区间分组:第1组:[20,25);第2组:[25,30);第3组:[30,35);第4组:[35,40);第5组:[40,45].得到的频率分布直方图如下图所示.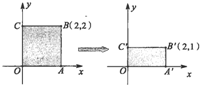 已知矩阵M=
已知矩阵M=