题目内容
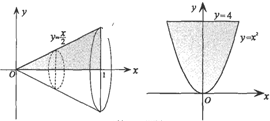
如图，在平面直角坐标系xOy中，将直线y=
与直线x=1及x轴所围成的图形旋转一周得到一个圆锥，圆锥的体积V圆锥=
π（
）2dx=
x3|
=
．
据此类推：将曲线y=x2与直线y=4所围成的图形绕y轴旋转一周得到一个旋转体，该旋转体的体积V= ．
| x |
| 2 |
| ∫ | 1 0 |
| x |
| 2 |
| π |
| 12 |
|
| π |
| 12 |
据此类推：将曲线y=x2与直线y=4所围成的图形绕y轴旋转一周得到一个旋转体，该旋转体的体积V=
考点：定积分在求面积中的应用
专题：计算题,函数的性质及应用
分析：根据题意，类比可得旋转体的体积V=
πydy，求出原函数，即可得出结论．
| ∫ | 4 0 |
解答：
解：由题意旋转体的体积V=
πydy=
y2
=8π，
故答案为：8π．
| ∫ | 4 0 |
| π |
| 2 |
| | | 4 0 |
故答案为：8π．
点评：本题给出曲线y=x2与直线y=4所围成的平面图形，求该图形绕xy轴转一周得到旋转体的体积．着重考查了利用定积分公式计算由曲边图形旋转而成的几何体体积的知识，属于基础题．
练习册系列答案
芒果教辅达标测试卷系列答案
相关题目
已知椭圆C：
+
=1（a＞b＞0）的左、右焦点分别是F1，F2，右顶点为A，上顶点为B，若椭圆C的中点到直线AB的距离为
|F1F2|，则椭圆C的离心率e=（ ）
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 6 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知函数y=f（x）是R上的减函数，且函数y=f（x-1）的图象关于点A（1，0）对称．设动点M（x，y），若实数x，y满足不等式 f（x2-8y+24）+f（y2-6x）≥0恒成立，则
•
的取值范围是（ ）
| OA |
| OM |
| A、（-∞，+∞） |
| B、[-1，1] |
| C、[2，4] |
| D、[3，5] |
数列{an}中，a1=1，a2n=n-an，a2n+1=an+1，则a100=（ ）
| A、30 | B、31 | C、32 | D、33 |
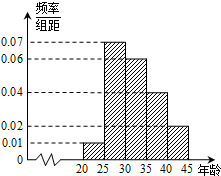某市为增强市民的环境保护意识，面向全市征召义务宣传志愿者，现从符合条件的志愿者中随机抽取100名，按年龄所在的区间分组：第1组：[20，25）；第2组：[25，30）；第3组：[30，35）；第4组：[35，40）；第5组：[40，45]．得到的频率分布直方图如下图所示．
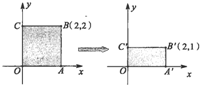已知矩阵M=