题目内容
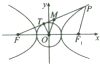 从双曲线
从双曲线| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||
| B、b-a | ||
C、
| ||
D、a+
|
考点:双曲线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:利用圆的切线的性质可得|FT|=
=
=b.再利用三角形的中位线定理、双曲线的定义可得:|OM|=
|PF1|,|TM|=
|PF|-|FT|,|PF|-|PF1|=2a,即可得出.
| |OF|2-|OT|2 |
| c2-a2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:
解:∵FT与⊙O相切于点T,
∴OT⊥FT.
∴|FT|=
=
=b.
∵点M是线段FP的中点,
∴|OM|=
|PF1|,|TM|=
|PF|-|FT|.
又|PF|-|PF1|=2a,
∴|OM|-|TM|=
(|PF1|-|PF|)+|FT|
=
×(-2a)+b
=b-a.
故选:B.
∴OT⊥FT.
∴|FT|=
| |OF|2-|OT|2 |
| c2-a2 |
∵点M是线段FP的中点,
∴|OM|=
| 1 |
| 2 |
| 1 |
| 2 |
又|PF|-|PF1|=2a,
∴|OM|-|TM|=
| 1 |
| 2 |
=
| 1 |
| 2 |
=b-a.
故选:B.
点评:本题考查了圆的切线的性质、三角形的中位线定理、双曲线的定义、勾股定理,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
对于函数y=f(x),部分x与y的对应关系如下表:
数列{xn}满足x1=2,且对任意n∈N*,点(xn,xn+1)都在函数y=f(x)的图象上,则x1+x2+x3+x4的值为( )
| x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| y | 7 | 4 | 5 | 8 | 1 | 3 | 5 | 2 | 6 |
| A、12 | B、14 | C、16 | D、18 |
若实数x,y满足条件
则2x-y的最小值为( )
|
| A、6 | B、3 | C、0 | D、-3 |
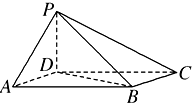 如图,四棱锥P-ABCD中,底面ABCD为平行四边形,∠DAB=60°,AB=2,AD=1,PD⊥底面ABCD.
如图,四棱锥P-ABCD中,底面ABCD为平行四边形,∠DAB=60°,AB=2,AD=1,PD⊥底面ABCD.