题目内容
对于函数y=f(x),部分x与y的对应关系如下表:
数列{xn}满足x1=2,且对任意n∈N*,点(xn,xn+1)都在函数y=f(x)的图象上,则x1+x2+x3+x4的值为( )
| x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| y | 7 | 4 | 5 | 8 | 1 | 3 | 5 | 2 | 6 |
| A、12 | B、14 | C、16 | D、18 |
考点:函数的值
专题:函数的性质及应用
分析:由已知得xn+1=f(xn),x1=2,x2=4,x3=8,x4=2,由此能求出x1+x2+x3+x4=2+4+8+2=16.
解答:
解:∵数列{xn}满足x1=2,且对任意n∈N*,点(xn,xn+1)都在函数y=f(x)的图象上,
∴xn+1=f(xn),
所以x1=2,x2=4,x3=8,x4=2,
∴x1+x2+x3+x4=2+4+8+2=16.
故选:C.
∴xn+1=f(xn),
所以x1=2,x2=4,x3=8,x4=2,
∴x1+x2+x3+x4=2+4+8+2=16.
故选:C.
点评:本题考查函数值的求法,是基础题,解题时要注意函数性质的合理运用.

练习册系列答案
相关题目
下列函数中,不满足f(2x)=2f(x)的是( )
| A、f(x)=x+1 |
| B、f(x)=x-|x| |
| C、f(x)=|x| |
| D、f(x)=-x |
命题“存在x0∈R,使sinx0+cosx0≤
”的否定是( )
| 2 |
A、任意x0∈R,都有sinx0+cosx0≤
| ||
B、任意x∈R,都有sinx+cosx>
| ||
C、存在x0∈R,使sinx0+cosx0>
| ||
D、任意x∈R,都有sinx+cosx≥
|
已知集合A={x||x|<1},B={x|log
x>0},则A∩B=( )
| 1 |
| 3 |
| A、(0,1) | B、(-1,1) |
| C、(1,+∞) | D、∅ |
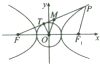 从双曲线
从双曲线| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||
| B、b-a | ||
C、
| ||
D、a+
|