题目内容
已知函数y=sin
(1-2cos2
),则导数y′= .
| x |
| 2 |
| x |
| 4 |
考点:导数的运算
专题:导数的综合应用
分析:利用倍角公式可得:函数y=sin
(1-2cos2
)=-sin
cos
=-
sinx,再利用导数的运算法则即可得出.
| x |
| 2 |
| x |
| 4 |
| x |
| 2 |
| x |
| 2 |
| 1 |
| 2 |
解答:
解:∵函数y=sin
(1-2cos2
)=-sin
cos
=-
sinx,
∴y′=-
cosx.
故答案为:-
cosx.
| x |
| 2 |
| x |
| 4 |
| x |
| 2 |
| x |
| 2 |
| 1 |
| 2 |
∴y′=-
| 1 |
| 2 |
故答案为:-
| 1 |
| 2 |
点评:本题考查了倍角公式、导数的运算法则,属于基础题.

练习册系列答案
相关题目
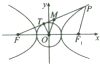 从双曲线
从双曲线| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||
| B、b-a | ||
C、
| ||
D、a+
|
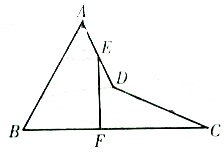 如图,在空间四边形ABCD中,两条对边AB=CD=3,E、F分别是另外两条对边AD,BC上的点,
如图,在空间四边形ABCD中,两条对边AB=CD=3,E、F分别是另外两条对边AD,BC上的点, 如图所示,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,作EP⊥PB交PB于点F
如图所示,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,作EP⊥PB交PB于点F