题目内容
若(
+
)n的展开式中前三项系数成等差数列.
(1)求展开式中所有的有理项;
(2)求展开式中二项式系数最大的项及系数最大的项.
| x |
| 1 | |||
2
|
(1)求展开式中所有的有理项;
(2)求展开式中二项式系数最大的项及系数最大的项.
考点:二项式系数的性质
专题:计算题,二项式定理
分析:(1)展开式中前三项的系数分别为1,
,
,成等差数列可得n的值,再写出通项,即可得出展开式中的有理项;
(2)运用二项式系数的性质,求解展开式中的二项式系数最大的项.设第k项的系数最大,列出不等式组,解得k的范围,再结合通项公式以及k为整数,求得展开式中系数最大的项.
| n |
| 2 |
| n(n-1) |
| 8 |
(2)运用二项式系数的性质,求解展开式中的二项式系数最大的项.设第k项的系数最大,列出不等式组,解得k的范围,再结合通项公式以及k为整数,求得展开式中系数最大的项.
解答:
(1)解:由于Tr+1=
•(
)n-r(
)r=
(
)rx
,
则展开式中前三项的系数分别为1,
,
,
则有2×
=1+
,解得n=8(1舍去).
则Tr+1=
(
)rx
,
则有r=0,4,8时,为有理项,且为x4,
•(
)4x=
x,
x-2.
(2)解:而n=8展开式共有9项,
中间一项二项式系数最大,即为T5=
x,
设第k项的系数最大,
则有
,解得 3≤k≤4,
故系数最大的项为第三项T3=7x
和 第四项T4=7x
.
| C | r n |
| x |
| 1 | |||
2
|
| C | r n |
| 1 |
| 2 |
| 2n-3r |
| 4 |
则展开式中前三项的系数分别为1,
| n |
| 2 |
| n(n-1) |
| 8 |
则有2×
| n |
| 2 |
| n(n-1) |
| 8 |
则Tr+1=
| C | r 8 |
| 1 |
| 2 |
| 16-3r |
| 4 |
则有r=0,4,8时,为有理项,且为x4,
| C | 4 8 |
| 1 |
| 2 |
| 35 |
| 8 |
| 1 |
| 256 |
(2)解:而n=8展开式共有9项,
中间一项二项式系数最大,即为T5=
| 35 |
| 8 |
设第k项的系数最大,
则有
|
故系数最大的项为第三项T3=7x
| 5 |
| 2 |
| 7 |
| 4 |
点评:本题考查二项式定理的应用及等差数列的性质,考查组合数的计算公式,二项展开式的通项公式,关键是掌握二项展开式的通项公式.

练习册系列答案
相关题目
命题“存在x0∈R,使sinx0+cosx0≤
”的否定是( )
| 2 |
A、任意x0∈R,都有sinx0+cosx0≤
| ||
B、任意x∈R,都有sinx+cosx>
| ||
C、存在x0∈R,使sinx0+cosx0>
| ||
D、任意x∈R,都有sinx+cosx≥
|
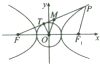 从双曲线
从双曲线| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||
| B、b-a | ||
C、
| ||
D、a+
|
若函数f(x)=
,若a•f(-a)<0,则实数a的取值范围是( )
|
| A、(-1,0)∪(1,+∞) |
| B、(-∞,-1)∪(0,1) |
| C、(-∞,-1)∪(1,+∞) |
| D、(-1,0)∪(0,1) |
 如图,在空间四边形ABCD中,两条对边AB=CD=3,E、F分别是另外两条对边AD,BC上的点,
如图,在空间四边形ABCD中,两条对边AB=CD=3,E、F分别是另外两条对边AD,BC上的点,