题目内容
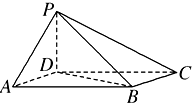 如图,四棱锥P-ABCD中,底面ABCD为平行四边形,∠DAB=60°,AB=2,AD=1,PD⊥底面ABCD.
如图,四棱锥P-ABCD中,底面ABCD为平行四边形,∠DAB=60°,AB=2,AD=1,PD⊥底面ABCD.(1)证明:PA⊥BD;
(2)若PD=AD,求二面角A-PB-D的正切值.
考点:二面角的平面角及求法,空间中直线与直线之间的位置关系
专题:空间位置关系与距离,空间角
分析:(1)因为∠DAB=60°,AB=2AD,由余弦定理得BD=
AD=
,由此能证明PA⊥BD.
(2)作AM垂直于PB于M点,连DM,则AD⊥平面PBD从而∠AMD为二面角A-PB-D的平面角,由此能求出其正切值.
| 3 |
| 3 |
(2)作AM垂直于PB于M点,连DM,则AD⊥平面PBD从而∠AMD为二面角A-PB-D的平面角,由此能求出其正切值.
解答:
 (1)证明:因为∠DAB=60°,AB=2AD,
(1)证明:因为∠DAB=60°,AB=2AD,
由余弦定理得BD=
AD=
,…(2分)
从而BD2+AD2=AB2,故BD⊥AD,…(3分)
∵PD⊥面ABCD,BD?面ABCD,∴PD⊥BD…(4分)
又AD∩PD=D,
所以BD⊥平面PAD…(5分)
故PA⊥BD.…(6分)
(2)解:作AM垂直于PB于M点,连DM,
由已知得AD⊥平面PBD
所以AD⊥BD,又AM⊥BD
BD⊥平面ADM所以BD⊥DM
所以∠AMD为二面角A-PB-D的平面角,
AD=1,DM=
,
tan∠AMD=
=
.
 (1)证明:因为∠DAB=60°,AB=2AD,
(1)证明:因为∠DAB=60°,AB=2AD,由余弦定理得BD=
| 3 |
| 3 |
从而BD2+AD2=AB2,故BD⊥AD,…(3分)
∵PD⊥面ABCD,BD?面ABCD,∴PD⊥BD…(4分)
又AD∩PD=D,
所以BD⊥平面PAD…(5分)
故PA⊥BD.…(6分)
(2)解:作AM垂直于PB于M点,连DM,
由已知得AD⊥平面PBD
所以AD⊥BD,又AM⊥BD
BD⊥平面ADM所以BD⊥DM
所以∠AMD为二面角A-PB-D的平面角,
AD=1,DM=
| ||
| 2 |
tan∠AMD=
| AD |
| DM |
| 2 |
| 3 |
| 3 |
点评:本题考查异面直线垂直的证明,考查二面角的正切值的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
 从双曲线
从双曲线| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||
| B、b-a | ||
C、
| ||
D、a+
|
若函数f(x)=log2a-1(a2-2a+1)的值为正数,则a的取值范围是( )
| A、(0,2) | ||
B、(0,
| ||
| C、(-∞,0)∪(2,+∞) | ||
D、(
|
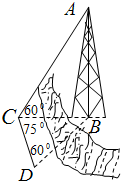 测量河对岸的塔高AB时,可以选与塔底B在同一水平面内的两个侧点C与D.现测得∠BCD=75°,∠BDC=60°,CD=100m.并在点C测得塔顶A的仰角∠ACB=60°,求:塔高AB.
测量河对岸的塔高AB时,可以选与塔底B在同一水平面内的两个侧点C与D.现测得∠BCD=75°,∠BDC=60°,CD=100m.并在点C测得塔顶A的仰角∠ACB=60°,求:塔高AB.