题目内容
已知圆锥的侧面展开图是半径为1且圆心角为π的扇形,则圆锥的体积为 .
考点:旋转体(圆柱、圆锥、圆台)
专题:空间位置关系与距离
分析:根据圆锥的侧面展开图扇形求出底面圆半径与圆锥的高,从而求出体积.
解答:
解:该圆锥的侧面展开图扇形的弧长为
π×1=2πr,
∴底面圆半径为r=
,
圆锥的高为
h=
=
=
;
∴圆锥的体积为
V=
Sh=
×π•(
)2×
=
π.
故答案为:
π.
π×1=2πr,
∴底面圆半径为r=
| 1 |
| 2 |
圆锥的高为
h=
| l2-r2 |
12-(
|
| ||
| 2 |
∴圆锥的体积为
V=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 24 |
故答案为:
| ||
| 24 |
点评:本题考查了空间几何体的体积的计算问题,解题时应根据空间几何体的特征进行计算,是基础题.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
已知集合A={x||x|<1},B={x|log
x>0},则A∩B=( )
| 1 |
| 3 |
| A、(0,1) | B、(-1,1) |
| C、(1,+∞) | D、∅ |
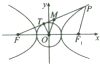 从双曲线
从双曲线| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||
| B、b-a | ||
C、
| ||
D、a+
|
不等式|
|<x的解集是( )
| x+1 |
| x-1 |
| A、{x|0x<1}∪{x|x>1} | ||||
B、{x|1-
| ||||
| C、{x|-1x<0} | ||||
D、{x|x>1+
|
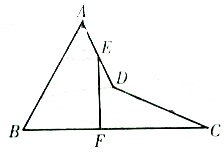 如图,在空间四边形ABCD中,两条对边AB=CD=3,E、F分别是另外两条对边AD,BC上的点,
如图,在空间四边形ABCD中,两条对边AB=CD=3,E、F分别是另外两条对边AD,BC上的点, 如图所示,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,作EP⊥PB交PB于点F
如图所示,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,作EP⊥PB交PB于点F