题目内容
已知f(logax)=
(x-
)(其中a是大于1的常数)
(1)求函数y=f(x)的解析式
(2)探讨函数y=f(x)的性质,并利用其性质解不等式f(1-m)+f(1-m2)<0.
| 1 |
| a-1 |
| 1 |
| x |
(1)求函数y=f(x)的解析式
(2)探讨函数y=f(x)的性质,并利用其性质解不等式f(1-m)+f(1-m2)<0.
考点:对数函数图象与性质的综合应用
专题:函数的性质及应用
分析:(1)设t=logax,a>1,t∈R则x=at,代入即可求解函数式子.(2)根据指数函数判断单调性,在运用奇偶性的定义判断为奇函数,即可求解1-m2<m-1,就能够得到答案.
解答:
解:(1)设t=logax,a>1,t∈R则x=at,
∵f(logax)=
(x-
)(其中a是大于1的常数)
∴f(t)=
(at-a-t),(其中a是大于1的常数)
∴函数y=f(x)=
(ax-a-x),(a>1,常数)
(2)∵f(-x)=)=
(a-x-ax)=-f(x),(a>1,常数)
∴f(x)为奇函数,
∵x1<x2,a x1<ax2,a -x1>a -x2,
∴a x1-ax2<0,a -x1-a -x2>0,
∴f(x1)-f(x2)=
((a x1-ax2)-(a -x1-a-x2))<0,
∴f(x1)<f(x2),
∴函数y=f(x)=
(ax-a-x),(a>1,常数)单调递增函数.
∵不等式f(1-m)+f(1-m2)<0.
∴1-m2<m-1,
m2+m-2>0,
即m>1或m<-2,
故不等式f(1-m)+f(1-m2)<0的解集为:(-∞,-2)∪(1,+∞)
∵f(logax)=
| 1 |
| a-1 |
| 1 |
| x |
∴f(t)=
| 1 |
| a-1 |
∴函数y=f(x)=
| 1 |
| a-1 |
(2)∵f(-x)=)=
| 1 |
| a-1 |
∴f(x)为奇函数,
∵x1<x2,a x1<ax2,a -x1>a -x2,
∴a x1-ax2<0,a -x1-a -x2>0,
∴f(x1)-f(x2)=
| 1 |
| a-1 |
∴f(x1)<f(x2),
∴函数y=f(x)=
| 1 |
| a-1 |
∵不等式f(1-m)+f(1-m2)<0.
∴1-m2<m-1,
m2+m-2>0,
即m>1或m<-2,
故不等式f(1-m)+f(1-m2)<0的解集为:(-∞,-2)∪(1,+∞)
点评:本题考察了指数函数的单调性,复合函数的奇偶性,单调性,运用解决不等式,属于中档题.

练习册系列答案
 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
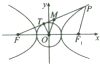 从双曲线
从双曲线| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||
| B、b-a | ||
C、
| ||
D、a+
|
不等式|
|<x的解集是( )
| x+1 |
| x-1 |
| A、{x|0x<1}∪{x|x>1} | ||||
B、{x|1-
| ||||
| C、{x|-1x<0} | ||||
D、{x|x>1+
|
若函数f(x)=
,若a•f(-a)<0,则实数a的取值范围是( )
|
| A、(-1,0)∪(1,+∞) |
| B、(-∞,-1)∪(0,1) |
| C、(-∞,-1)∪(1,+∞) |
| D、(-1,0)∪(0,1) |