题目内容
已知△ABC的顶点A(3,0),B(0,1),C(1,1),P(x,y)在△ABC内部(包括边界),若目标函数z=
(a≠0)取得最大值时的最优解有无穷多组,则点(a,b)的轨迹可能是( )
| ax+by |
| c |
A、 |
B、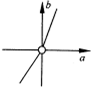 |
C、 |
D、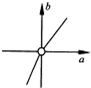 |
考点:简单线性规划
专题:不等式的解法及应用
分析:作出三角形对应的区域,求出对应的直线斜率,根据目标函数取得最优解的个数有无穷多组,则得到目标函数的斜率与三角形对应边的斜率存在一定的关系,即可得到结论.
解答:
解:作出△ABC对应的平面区域如图:则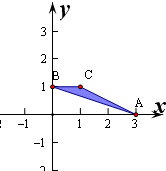 AB的斜率kAB=
AB的斜率kAB=
=-
,
AC的斜率kAC=
=-
,
目标函数z=
(a≠0)等价为ax+by=zc,
即y=-
x+
z,
若目标函数z=
(a≠0)取得最大值时的最优解有无穷多组,
则目标函数的斜率k=kAB或者k=kAC,
即-
=-
或-
=-
,
即b=3a或b=2a,(a≠0),
则点(a,b)的轨迹可能是A,
故选:A
 AB的斜率kAB=
AB的斜率kAB=| 1-0 |
| 0-3 |
| 1 |
| 3 |
AC的斜率kAC=
| 1-0 |
| 1-3 |
| 1 |
| 2 |
目标函数z=
| ax+by |
| c |
即y=-
| a |
| b |
| c |
| b |
若目标函数z=
| ax+by |
| c |
则目标函数的斜率k=kAB或者k=kAC,
即-
| a |
| b |
| 1 |
| 3 |
| a |
| b |
| 1 |
| 2 |
即b=3a或b=2a,(a≠0),
则点(a,b)的轨迹可能是A,
故选:A
点评:本题主要考查线性规划以及直线斜率的应用,根据目标函数取得最优解的个数,确定目标函数的斜率关系是解决本题的关键.

练习册系列答案
相关题目
若平面α∥平面β,直线a∥平面α,点B∈β,则在平面β内且过B点的所有直线中( )
| A、不一定存在与a平行的直线 |
| B、只有两条与a平行的直线 |
| C、存在无数条与a平行的直线 |
| D、存在唯一与a平行的直线 |
x=2是x2-4x+4=0的( )
| A、充分条件 |
| B、必要条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
“a=1”是“函数f(x)=(x-1)2在区间[a,+∞)上为增函数”的( )
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
在△ABC中,“cosA=cosB”是“sinA=sinB”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
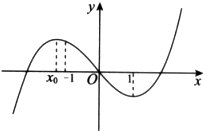 函数f(x)=ax3-bx2+cx的图象如图所示,且f(x)在x=x0与x=1处取得极值,给出下列判断:
函数f(x)=ax3-bx2+cx的图象如图所示,且f(x)在x=x0与x=1处取得极值,给出下列判断:①c>0;
②f(1)+f(-1)>0;
③函数y=f′(x)在区间(0,+∞)上是增函数.
其中正确的判断是( )
| A、①③ | B、② | C、②③ | D、①② |
命题“对任意实数x,都有x>1”的否定是( )
| A、对任意实数x,都有x<1 |
| B、不存在实数x,使x≤1 |
| C、对任意实数x,都有x≤1 |
| D、存在实数x,使x≤1 |