题目内容
利用三角函数线求下列函数的定义域.
(1)y=
;
(2)y=lg(1-4cos2x)
(1)y=
2sin(x)-
|
(2)y=lg(1-4cos2x)
考点:余弦函数的定义域和值域,正弦函数的定义域和值域
专题:三角函数的图像与性质
分析:分别由根式和对数有意义,结合三角函数线可得.
解答:
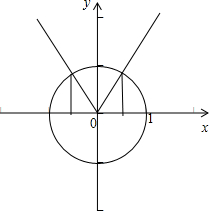
解:(1)由根式有意义可得2sinx-
≥0,
变形可得sinx≥
,
由三角函数线可得函数的定义域为{x|
+2kπ≤x≤
+2kπ,k∈Z};
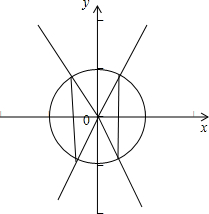
(2)由对数有意义可得1-4cos2x>0,
变形可得cos2x<
,解得-
<cos<
,
由三角函数线可得函数的定义域为{x|
+2kπ≤x≤
+2kπ,k∈Z}∪{x|
+2kπ≤x≤
+2kπ,k∈Z}
| 3 |
变形可得sinx≥
| ||
| 2 |
由三角函数线可得函数的定义域为{x|
| π |
| 3 |
| 2π |
| 3 |

(2)由对数有意义可得1-4cos2x>0,
变形可得cos2x<
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
由三角函数线可得函数的定义域为{x|
| π |
| 3 |
| 2π |
| 3 |
| 4π |
| 3 |
| 5π |
| 3 |

点评:本题考查函数的定义域,涉及三角函数线的应用,属基础题.

练习册系列答案
相关题目
已知△ABC的顶点A(3,0),B(0,1),C(1,1),P(x,y)在△ABC内部(包括边界),若目标函数z=
(a≠0)取得最大值时的最优解有无穷多组,则点(a,b)的轨迹可能是( )
| ax+by |
| c |
A、 |
B、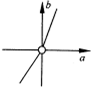 |
C、 |
D、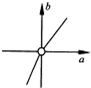 |
已知一个容量为40的数据样本,分组后,组距与频率如下:[20,30),4个;[30,40),6个;[40,50),8个;[50,60),9个[60,70),7个;[70,80),6个.则样本在区间[60,+∞)上的频率是( )
| A、10% | B、20% |
| C、32.5% | D、40% |
当θ是第四象限时,两直线xsinθ+y
-a=0和x+y
+b=0的位置关系是( )
| 1+cosθ |
| 1-cosθ |
| A、平行 | B、垂直 |
| C、相交但不垂直 | D、重合 |
