题目内容
命题“对任意实数x,都有x>1”的否定是( )
| A、对任意实数x,都有x<1 |
| B、不存在实数x,使x≤1 |
| C、对任意实数x,都有x≤1 |
| D、存在实数x,使x≤1 |
考点:命题的否定
专题:简易逻辑
分析:全称命题的否定是特称命题,写出结果即可.
解答:
解:因为全称命题的否定是特称命题,所以命题“对任意实数x,都有x>1”的否定是:存在实数x,使x≤1.
故选:D.
故选:D.
点评:本题考查命题的否定,全称命题与特称命题的否定关系.

练习册系列答案
相关题目
已知△ABC的顶点A(3,0),B(0,1),C(1,1),P(x,y)在△ABC内部(包括边界),若目标函数z=
(a≠0)取得最大值时的最优解有无穷多组,则点(a,b)的轨迹可能是( )
| ax+by |
| c |
A、 |
B、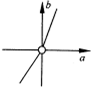 |
C、 |
D、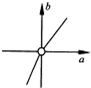 |
设a,b,c∈(-∞,0),则a+
,b+
,c+
( )
| 4 |
| b |
| 4 |
| c |
| 4 |
| a |
| A、都不大于-4 |
| B、都不小于-4 |
| C、至少有一个不大于-4 |
| D、至少有一个不小于-4 |
已知θ是钝角三角形中的最小角,则sin(θ+
)的取值范围是( )
| π |
| 3 |
A、(
| ||||
B、[
| ||||
C、(
| ||||
D、[
|
已知从A口袋中摸出一个球是红球的概率为
,从B口袋中摸出一个球是红球的概率为
.现从两个口袋中各摸出一个球,那么这两个球中没有红球的概率是( )
| 1 |
| 3 |
| 2 |
| 5 |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知一个容量为40的数据样本,分组后,组距与频率如下:[20,30),4个;[30,40),6个;[40,50),8个;[50,60),9个[60,70),7个;[70,80),6个.则样本在区间[60,+∞)上的频率是( )
| A、10% | B、20% |
| C、32.5% | D、40% |
当θ是第四象限时,两直线xsinθ+y
-a=0和x+y
+b=0的位置关系是( )
| 1+cosθ |
| 1-cosθ |
| A、平行 | B、垂直 |
| C、相交但不垂直 | D、重合 |
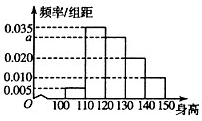 从某小学随机抽取100名学生,将他们的身高(单位:厘米)数据绘制成频率分布直方图(如图),若要从身高在[120,130),[130,140),[140,150]三组内的学生中,用分层抽样的方法选取20人参加一项活动,则从身高在[120,130)内的学生中选取的人数应为
从某小学随机抽取100名学生,将他们的身高(单位:厘米)数据绘制成频率分布直方图(如图),若要从身高在[120,130),[130,140),[140,150]三组内的学生中,用分层抽样的方法选取20人参加一项活动,则从身高在[120,130)内的学生中选取的人数应为