题目内容
在△ABC中，“cosA=cosB”是“sinA=sinB”的（ ）
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
考点：必要条件、充分条件与充要条件的判断
专题：简易逻辑
分析：根据三角函数的性质以及充分条件和必要条件的定义即可得到结论．
解答：
解：在△ABC中，若cosA=cosB，则A=B，则sinA=sinB成立，即充分性成立，
若sinA=sinB，则A=B，则cosA=cosB成立，即必要性成立，
则，“cosA=cosB”是“sinA=sinB”的充要条件，
故选：C
若sinA=sinB，则A=B，则cosA=cosB成立，即必要性成立，
则，“cosA=cosB”是“sinA=sinB”的充要条件，
故选：C
点评：本题主要考查充分条件和必要条件的判断，根据三角函数的性质是解决本题的关键．
练习册系列答案
相关题目
下列哪个函数与y=x是相同函数（ ）
A、y=
| |||
B、y=
| |||
C、y=
| |||
| D、y=alogax（a＞0且a≠1） |
已知函数f（x）在x∈R上恒有f（-x）=f（x），若对于x≥0，都有f（x+2）=f（x），且当x∈[0，2）时，f（x）=log2（x+1），则f（-2014）+f（2015）的值为（ ）
| A、-2 | B、-1 | C、1 | D、2 |
已知△ABC的顶点A（3，0），B（0，1），C（1，1），P（x，y）在△ABC内部（包括边界），若目标函数z=
（a≠0）取得最大值时的最优解有无穷多组，则点（a，b）的轨迹可能是（ ）
| ax+by |
| c |
A、 |
B、 |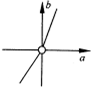
C、 |
D、 |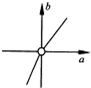
若二面角M-l-N的平面角大小为
π，直线m⊥平面M，则平面N内的直线与m所成角的取值范围是（ ）
| 2 |
| 3 |
A、[
| ||||
B、[
| ||||
C、[
| ||||
D、[0，
|
设a，b，c∈（-∞，0），则a+
，b+
，c+
（ ）
| 4 |
| b |
| 4 |
| c |
| 4 |
| a |
| A、都不大于-4 |
| B、都不小于-4 |
| C、至少有一个不大于-4 |
| D、至少有一个不小于-4 |
已知从A口袋中摸出一个球是红球的概率为
，从B口袋中摸出一个球是红球的概率为
．现从两个口袋中各摸出一个球，那么这两个球中没有红球的概率是（ ）
| 1 |
| 3 |
| 2 |
| 5 |
A、
| ||
B、
| ||
C、
| ||
D、
|