题目内容
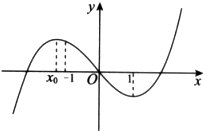函数f（x）=ax3-bx2+cx的图象如图所示，且f（x）在x=x0与x=1处取得极值，给出下列判断：①c＞0；
②f（1）+f（-1）＞0；
③函数y=f′（x）在区间（0，+∞）上是增函数．
其中正确的判断是（ ）
| A、①③ | B、② | C、②③ | D、①② |
考点：利用导数研究函数的单调性
专题：导数的综合应用
分析：求出函数的导数，根据f（x）在x=x0与x=1处取得极值，求出a，b，c之间的关系，即可得到结论．
解答：
解：∵函数f（x）=ax3-bx2+cx，且f（x）在x=x0与x=1处取得极值，
∴a＞0，且f′（x）=3ax2-2bx+c，
则x=x0与x=1是方程f′（x）=3ax2-2bx+c=0的两个不同的根，
即1+x0=
，1×x0=
，
则2b=3a（1+x0），c=3ax0，
∵由图象可知x0＜-1，∴c=3ax0＜0，故①不正确．
∵f（1）+f（-1）=-2b，且2b=3a（1+x0）＜0，
∴f（1）+f（-1）=-2b＞0，故②正确．
f′（x）=3ax2-2bx+c=3a（x-1）（x-x0）是开口向上，对称轴为x=-
=
＜0
∴函数y=f′（x）在区间（0，+∞）上是增函数，故③正确
故正确的命题是②③，
故选：C
∴a＞0，且f′（x）=3ax2-2bx+c，
则x=x0与x=1是方程f′（x）=3ax2-2bx+c=0的两个不同的根，
即1+x0=
| 2b |
| 3a |
| c |
| 3a |
则2b=3a（1+x0），c=3ax0，
∵由图象可知x0＜-1，∴c=3ax0＜0，故①不正确．
∵f（1）+f（-1）=-2b，且2b=3a（1+x0）＜0，
∴f（1）+f（-1）=-2b＞0，故②正确．
f′（x）=3ax2-2bx+c=3a（x-1）（x-x0）是开口向上，对称轴为x=-
| -2b |
| 2×3a |
| b |
| 3a |
∴函数y=f′（x）在区间（0，+∞）上是增函数，故③正确
故正确的命题是②③，
故选：C
点评：本题主要考查导数研究函数的应用，求出函数的导数，结合二次函数的性质，判断a，b，c的大小是解决本题的关键．
练习册系列答案
阅读快车系列答案
相关题目
设曲线y=ax2+2014在点（1，a+2014）处的切线与直线2x-y-2015=0平行，则a=（ ）
| A、1 | ||
B、
| ||
C、-
| ||
| D、-1 |
已知△ABC的顶点A（3，0），B（0，1），C（1，1），P（x，y）在△ABC内部（包括边界），若目标函数z=
（a≠0）取得最大值时的最优解有无穷多组，则点（a，b）的轨迹可能是（ ）
| ax+by |
| c |
A、 |
B、 |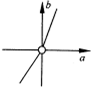
C、 |
D、 |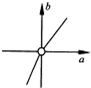
已知曲线C的参数方程
（t为参数），C在点（1，1）处的切线为l，以坐标原点为极点，x轴的正半轴为极轴建立极坐标系，则l的极坐标方程为（ ）
|
A、ρ=
| ||||
B、ρsin（θ+
| ||||
C、ρsin（θ+
| ||||
D、ρ=sin（θ+
|
设a，b，c∈（-∞，0），则a+
，b+
，c+
（ ）
| 4 |
| b |
| 4 |
| c |
| 4 |
| a |
| A、都不大于-4 |
| B、都不小于-4 |
| C、至少有一个不大于-4 |
| D、至少有一个不小于-4 |
已知θ是钝角三角形中的最小角，则sin（θ+
）的取值范围是（ ）
| π |
| 3 |
A、（
| ||||
B、[
| ||||
C、（
| ||||
D、[
|