题目内容
已知函数f (x)=
则满足f (a)<
的a的取值范围是( )
|
| 1 |
| 2 |
A、(-∞,-1)∪(0,
| ||
| B、(-∞,-1) | ||
C、(0,
| ||
| D、(-∞,-1)∪(0,2) |
考点:分段函数的应用
专题:计算题,函数的性质及应用,不等式的解法及应用
分析:由题意可得,f (a)<
等价为
或
,分别解出它们,最后求并集即可.
| 1 |
| 2 |
|
|
解答:
解:f (a)<
等价为
或
,
即有
或
,
则a<-1或0<a<
,
故选A.
| 1 |
| 2 |
|
|
即有
|
|
则a<-1或0<a<
| 2 |
故选A.
点评:本题考查分段函数及运用,考查分段函数值注意各段的范围,考查指数不等式和对数不等式的解法,属于中档题.

练习册系列答案
相关题目
已知函数f(x)=
是R上的增函数,那么实数a的取值范围为( )
|
A、(
| ||
| B、(1,+∞) | ||
| C、[2,+∞) | ||
| D、(1,2) |
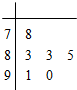 对某同学的6次数学测试成绩(满分100分)进行统计,作出的茎叶图如图所示,给出关于该同学数学成绩的以下说法:
对某同学的6次数学测试成绩(满分100分)进行统计,作出的茎叶图如图所示,给出关于该同学数学成绩的以下说法:①中位数为84;
②众数为85;
③平均数为85;
④极差为12.
其中,正确说法的序号是( )
| A、①② | B、③④ | C、②④ | D、①③ |
函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
)的部分图象如图示,则下列说法不正确的是( )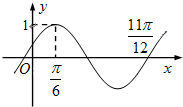
| π |
| 2 |

| A、ω=2 | ||||
B、f(x)的图象关于点(
| ||||
C、k(x)=f(
| ||||
| D、已知函数g(x)=cos(ξx+η)图象与f(x)的对称轴完全相同,则ξ=2 |
已知k∈[-2,1],则k的值使得过A(1,1)可以作两条直线与圆 x2+y2+kx-2y-
k=0相切的概率等于( )
| 5 |
| 4 |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知函数f(x)在R上满足f(x)=2f(-x)-x2则曲线y=f(x)在点(1,f(1))处的切线方程是( )
| A、y=x |
| B、y=2x-1 |
| C、y=3x-2 |
| D、y=-2x+3 |