题目内容
函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
)的部分图象如图示,则下列说法不正确的是( )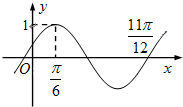
| π |
| 2 |

| A、ω=2 | ||||
B、f(x)的图象关于点(
| ||||
C、k(x)=f(
| ||||
| D、已知函数g(x)=cos(ξx+η)图象与f(x)的对称轴完全相同,则ξ=2 |
考点:正弦函数的图象,正弦函数的单调性,正弦函数的对称性
专题:三角函数的求值,三角函数的图像与性质
分析:首先根据函数的图象求出解析式,进一步利用函数的单调性、周期、对称中心求出结果.
解答:
解:根据函数的图象:
=
,
所以:T=π,
利用T=
,
解得:ω=2;
当x=
时,f(
)=1,
解得:A=1,Φ=
,
所以f(x)=sin(2x+
);
所以:①A正确
②B令2x+
=kπ,
解得:x=
-
,
当k=1时,对称中心为:(
,0);
③g(x)=cos(ξx+η)图象与f(x)的对称轴完全相同,则ξ=2,由于η不确定.
④函数的区间有增有减.
故选:C
| 3T |
| 4 |
| 3π |
| 4 |
所以:T=π,
利用T=
| 2π |
| ω |
解得:ω=2;
当x=
| π |
| 6 |
| π |
| 6 |
解得:A=1,Φ=
| π |
| 6 |
所以f(x)=sin(2x+
| π |
| 6 |
所以:①A正确
②B令2x+
| π |
| 6 |
解得:x=
| kπ |
| 2 |
| π |
| 12 |
当k=1时,对称中心为:(
| 5π |
| 12 |
③g(x)=cos(ξx+η)图象与f(x)的对称轴完全相同,则ξ=2,由于η不确定.
④函数的区间有增有减.
故选:C
点评:本题考查的知识要点:函数解析式的确定,函数的单调性、周期、对称中心的应用.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
已知函数f (x)=
则满足f (a)<
的a的取值范围是( )
|
| 1 |
| 2 |
A、(-∞,-1)∪(0,
| ||
| B、(-∞,-1) | ||
C、(0,
| ||
| D、(-∞,-1)∪(0,2) |
已知二次函数f(x)=ax2+bx(a≠0)满足1≤f(-1)≤2,2≤f(1)≤4,则f(-2)的范围是( )
| A、[3,12] |
| B、(3,12) |
| C、(5,10) |
| D、[5,10] |