题目内容
顶点在原点,经过圆C:x2+y2-2x+2
y=0的圆心且准线与x轴垂直的抛物线方程为 .
| 2 |
考点:抛物线的标准方程
专题:圆锥曲线的定义、性质与方程
分析:设出抛物线方程,利用经过点(2,2),求出抛物线中的参数,即可得到抛物线方程.
解答:
解:因为圆C:x2+y2-2x+2
y=0的圆心是(1,-
)
抛物线的顶点在原点,焦点在x轴上,且经过点(1,-
),
设标准方程为y2=2px,
因为点(1,-
)在抛物线上,所以(-
)2=2p,
所以p=1,
所以所求抛物线方程为:y2=2x.
故答案为:y2=2x.
| 2 |
| 2 |
抛物线的顶点在原点,焦点在x轴上,且经过点(1,-
| 2 |
设标准方程为y2=2px,
因为点(1,-
| 2 |
| 2 |
所以p=1,
所以所求抛物线方程为:y2=2x.
故答案为:y2=2x.
点评:本题是基础题,考查抛物线的标准方程的求法,注意标准方程的形式,是易错题,考查计算能力.

练习册系列答案
相关题目
锐角△ABC中,角A,B,C所对的边分别为a,b,c,若C=2A,则
的取值范围是( )
| c |
| a |
A、(
| ||||
B、(1,
| ||||
C、(
| ||||
| D、(1,2) |
从甲、乙、丙三人中任选2人作代表,则甲被选中的概率为( )
A、
| ||
B、
| ||
C、
| ||
| D、1 |
已知函数f (x)=
则满足f (a)<
的a的取值范围是( )
|
| 1 |
| 2 |
A、(-∞,-1)∪(0,
| ||
| B、(-∞,-1) | ||
C、(0,
| ||
| D、(-∞,-1)∪(0,2) |
已知二次函数f(x)=ax2+bx(a≠0)满足1≤f(-1)≤2,2≤f(1)≤4,则f(-2)的范围是( )
| A、[3,12] |
| B、(3,12) |
| C、(5,10) |
| D、[5,10] |
若x∈(1,10),a=lgx,b=2lgx,c=lg2x,d=lg(lgx),则( )
| A、a<b<c<d |
| B、d<c<a<b |
| C、d<b<a<c |
| D、b<d<c<a |
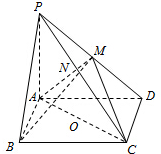 在四棱锥P-ABCD中,底面ABCD是矩形PA⊥ABCD,PA=AD=4,AB=2.以AC的中点O为球心、AC为直径的球面交PD于点M,交PC于点N.
在四棱锥P-ABCD中,底面ABCD是矩形PA⊥ABCD,PA=AD=4,AB=2.以AC的中点O为球心、AC为直径的球面交PD于点M,交PC于点N.