题目内容
已知不等式|x+4|+|x-m|≤5的解集为{x|-4≤x≤1}.
(Ⅰ)求m的值;
(Ⅱ)若a2+2b2+3c2=m,求a+4b+9c的最值.
(Ⅰ)求m的值;
(Ⅱ)若a2+2b2+3c2=m,求a+4b+9c的最值.
考点:绝对值不等式的解法,二维形式的柯西不等式
专题:计算题,不等式的解法及应用
分析:(Ⅰ)由于|x+4|+|x-m|表示数轴上的x对应点到-4和m对应点的距离之和,而-4、1对应点距离之和正好等于5,由此求得m的解;
(Ⅱ)可令
=(1,2
,3
),
=(a,
b,
c),运用不等式|
•
|=|
|•|
|•|cos<
,
>|≤|
|•|
|,计算即可得到最值.
(Ⅱ)可令
| m |
| 2 |
| 3 |
| n |
| 2 |
| 3 |
| m |
| n |
| m |
| n |
| m |
| n |
| m |
| n |
解答:
解:(Ⅰ)根据绝对值的几何意义可得,
|x+4|+|x-m|表示数轴上的x对应点到-4和m对应点的距离之和,
而-4、1对应点距离之和正好等于5,
∴m=1.
(Ⅱ)由(Ⅰ)得a2+2b2+3c2=1.
可令
=(1,2
,3
),
=(a,
b,
c),
则
•
=a+4b+9c,|
|=
=6,|
|=
,
由于|
•
|=|
|•|
|•|cos<
,
>|≤|
|•|
|,
当
,
共线时,取得等号.
则|a+4b+9c|≤6
=6
则有-6≤a+4b+9c≤6,
则a+4b+9c的最小值为-6,最大值为6.
|x+4|+|x-m|表示数轴上的x对应点到-4和m对应点的距离之和,
而-4、1对应点距离之和正好等于5,
∴m=1.
(Ⅱ)由(Ⅰ)得a2+2b2+3c2=1.
可令
| m |
| 2 |
| 3 |
| n |
| 2 |
| 3 |
则
| m |
| n |
| m |
| 1+8+27 |
| n |
| a2+2b2+3c2 |
由于|
| m |
| n |
| m |
| n |
| m |
| n |
| m |
| n |
当
| m |
| n |
则|a+4b+9c|≤6
| a2+2b2+3c2 |
则有-6≤a+4b+9c≤6,
则a+4b+9c的最小值为-6,最大值为6.
点评:本题考查绝对值不等式的解法,考查绝对值的几何意义,考查运用向量法求最值,考查运算能力,属于中档题.

练习册系列答案
相关题目
设f(x)=|x-a|是偶函数,g(x)=2x+
是奇函数,那么a+b的值为( )
| b |
| 2x |
A、-
| ||
B、
| ||
| C、-1 | ||
| D、1 |
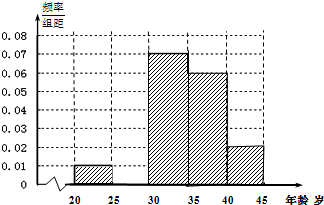 某市要对两千多名出租车司机的年龄进行调查,现从中随机抽出100名司机,已知抽到的司机年龄都在[20,45)岁之间,根据调查结果得出司机的年龄情况残缺的频率分布直方图如图所示,利用这个残缺的频率分布直方图估计该市出租车司机年龄的中位数大约是
某市要对两千多名出租车司机的年龄进行调查,现从中随机抽出100名司机,已知抽到的司机年龄都在[20,45)岁之间,根据调查结果得出司机的年龄情况残缺的频率分布直方图如图所示,利用这个残缺的频率分布直方图估计该市出租车司机年龄的中位数大约是
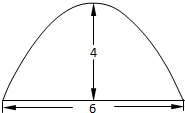 如图,一个抛物线型拱桥,当水面离拱顶4m时,水面的宽6m.经过一段时间的降雨后,水面上升了1m,此时水面宽度为
如图,一个抛物线型拱桥,当水面离拱顶4m时,水面的宽6m.经过一段时间的降雨后,水面上升了1m,此时水面宽度为