题目内容
某几何体的三视图（单位：cm）如图所示，则此几何体的侧视图面积为 cm2，此几何体的体积为 cm3．
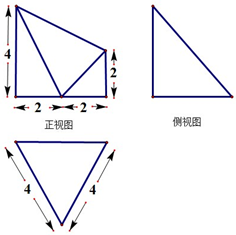
考点：由三视图求面积、体积
专题：计算题,空间位置关系与距离
分析：由已知中的三视图可知：该几何体是以正视图为底面的四棱锥，计算出几何体的底面面积和高，代入棱锥体积公式，可得答案．
解答：
解：几何体的侧视图是直角三角形，直角边长为4，2
，面积为
×4×2
=4
由已知中的三视图可知：该几何体是以正视图为底面的四棱锥，
其底面面积S=
×（2+4）×4=12，棱锥的高h=2
，
故棱锥的体积V=
×12×2
=8
，
故答案为：4
，8
．
| 3 |
| 1 |
| 2 |
| 3 |
| 3 |
由已知中的三视图可知：该几何体是以正视图为底面的四棱锥，
其底面面积S=
| 1 |
| 2 |
| 3 |
故棱锥的体积V=
| 1 |
| 3 |
| 3 |
| 3 |
故答案为：4
| 3 |
| 3 |
点评：本题考查了由三视图求几何体的体积，判断几何体的形状及数据所对应的几何量是解答此类问题的关键．
练习册系列答案
相关题目
下面伪代码表示的算法中，最后一次输出的I的值是 （ ）
| A、5 | B、8 | C、11 | D、14 |
在两个袋内，分别写着装有1，2，3，4，5，6六个数字的6张卡片，今从每个袋中各取一张卡片，则两数之间和能被3整除的概率为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
已知|
|=2|
|≠0，且关于x的方程x2+|
|x+
•
=0有实根，则向量
与
的夹角的取值范围是（ ）
| a |
| b |
| a |
| a |
| b |
| a |
| b |
A、[
| ||||
B、[0，
| ||||
C、[
| ||||
D、[
|