题目内容
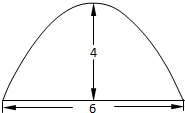如图，一个抛物线型拱桥，当水面离拱顶4m时，水面的宽6m．经过一段时间的降雨后，水面上升了1m，此时水面宽度为考点：抛物线的应用
专题：计算题,圆锥曲线的定义、性质与方程
分析：建立直角坐标系，设抛物线为y=ax2，把点（3，-4）代入求出解析式，根据当y=-3时，求出x的值，即可得出水面宽度．
解答：
解：如图，建立直角坐标系，
可设这条抛物线为y=ax2，
把点（3，-4）代入，得-4=a×32，a=-
，
∴y=-
x2，
当y=-3时，-3=-
x2，x=±
，
∴水面上升1m，水面宽度为3
m．
故答案为：3
．
解：如图，建立直角坐标系，可设这条抛物线为y=ax2，
把点（3，-4）代入，得-4=a×32，a=-
| 4 |
| 9 |
∴y=-
| 4 |
| 9 |
当y=-3时，-3=-
| 4 |
| 9 |
3
| ||
| 2 |
∴水面上升1m，水面宽度为3
| 3 |
故答案为：3
| 3 |
点评：此题主要考查了抛物线的应用，根据已知建立坐标系从而得出抛物线解析式是解决问题的关键．
练习册系列答案
阅读快车系列答案
相关题目
已知|
|=2|
|≠0，且关于x的方程x2+|
|x+
•
=0有实根，则向量
与
的夹角的取值范围是（ ）
| a |
| b |
| a |
| a |
| b |
| a |
| b |
A、[
| ||||
B、[0，
| ||||
C、[
| ||||
D、[
|
用a，b，c表示三条不同的直线，γ表示平面，给出下列命题：
①若a∥b，b∥c，则a∥c； ②若a⊥b，b⊥c，则a⊥c；
③若a∥γ，b∥γ，则a∥b； ④若a⊥γ，b⊥γ，则a∥b．其中真命题的序号是（ ）
①若a∥b，b∥c，则a∥c； ②若a⊥b，b⊥c，则a⊥c；
③若a∥γ，b∥γ，则a∥b； ④若a⊥γ，b⊥γ，则a∥b．其中真命题的序号是（ ）
| A、①② | B、②③ | C、①④ | D、③④ |
动点P（x，y，z）的坐标始终满足y=3，则动点P的轨迹为（ ）
| A、y轴上一点 |
| B、坐标平面xOz |
| C、与坐标平面xOz平行的一个平面 |
| D、平行于y轴的一条直线 |
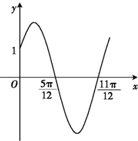已知函数f（x）=Asin（ωx+φ）（x∈R，ω＞0，0＜φ＜