已知正六边形ABCDEF.边长为1.其中心为O．(1)在A.B.C.D.E.F.0中任取2点.作为向量的起点和终点.求得到单位向量的概率,(2)在A.B.C.D.E.F中任取3点.求构成三角形的面积为34的概率．题目和参考答案——青夏教育精英家教网—

题目内容

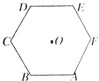已知正六边形ABCDEF，边长为1，其中心为O．
（1）在A、B、C、D、E、F、0中任取2点，作为向量的起点和终点，求得到单位向量的概率；
（2）在A、B、C、D、E、F中任取3点，求构成三角形的面积为

的概率．

考点：列举法计算基本事件数及事件发生的概率

专题：概率与统计

分析：（1）利用单位向量的定义可得：单位向量为以O为端点、每一条边所在的向量有24个；同理可得：模为

的向量有12个，模为2的有6个，利用古典概型的概率计算公式即可得出．
（2）在A、B、C、D、E、F中任取3点，构成三角形的面积为

有6个为△ABC，△BCD，△CDE，△DEF，△EFA，△FAB，同理可得面积为

的三角形有12个，面积为

的三角形有2个，共有20个．构成三角形的面积为

的概率P=

．

解答： 解：（1）在A、B、C、D、E、F、0中任取2点，作为向量的起点和终点，
其中单位向量为以O为端点、每一条边所在的向量有24个；同理可得：模为

的向量有12个，模为2的有6个，
以上共有42个向量．
∴得到单位向量的概率P=

．
（2）在A、B、C、D、E、F中任取3点，构成三角形的面积为

有6个，面积为

的三角形有12个，面积为

的三角形有2个，共有20个．构成三角形的面积为

的概率P=

．

点评：本题考查了单位向量、向量的模、三角形的面积计算公式、古典概型的概率计算公式，考查了分类讨论的思想方法，考查了计算能力，属于基础题．

练习册系列答案

68所名校图书小升初高分夺冠真卷系列答案

已知函数f（x）=a1nx-ax-3（a≠0）
（1）讨论函数f（x）的单调性；
（2）若函数y=f（x）的图象在点（2，f（2））处的切线的倾斜角为45°，那么实数m在什么范围取值时，函数g(x)=x3+x2[

+f′(x)]在区间（2，3）内总存在极值？
（3）求证：

已知二次函数f（x）的二次项系数为正且f（2-x）=f（2+x）．求不等式f（2-

x²）＜f（-x²+6x-7）的解集．

已知函数f（x）=a^x（a＞0且a≠1）
（1）若f（x₀）=2，求f（3x₀）的值；
（2）若f（x²-3x+1）≤f（x²+2x-4），求x的取值范围．

从原点向圆x²+y²-12y+27=0作两条切线，则这两个切点之间的距离为

．

若A₁，A₂，…，A_m为集合A={1，2，…，n}（n≥2且n∈N^*）的子集，且满足两个条件：
①A₁∪A₂∪…∪A_m=A；
②对任意的{x，y}⊆A，至少存在一个i∈{1，2，3，…，m}，使A_i∩{x，y}={x}或{y}．则称集合组A₁，A₂，…，A_m具有性质P．
如图，作n行m列数表，定义数表中的第k行第l列的数为a_ki=

1(k∈Ai)

0(k∉Ai)

a₁₁	a₁₂	…	a_1m
a₂₁	a₂₂	…	a_2m
?	?	?	?
a_n1	a_n2	…	a_nm

（Ⅰ）当n=4时，判断下列两个集合组是否具有性质P，如果是请画出所对应的表格，如果不是请说明理由；
集合组1：A₁={1，3}，A2={2，3}，A3={4}；集合组2：A1={2，3，4}，A2={2，3}，A3={1，4}．
（Ⅱ）当n=7时，若集合组A₁，A₂，A₃具有性质P，请先画出所对应的7行3列的一个数表，再依此表格分别写出集合A₁，A₂，A₃；
（Ⅲ）当n=100时，集合组A₁，A₂，…，A_t是具有性质P且所含集合个数最小的集合组，求t的值及|A₁|+|A₂|+…|A_t|的最小值．（其中|A_i|表示集合A_i所含元素的个数）

已知x∈R，求

x2+4

的取值范围．

试题分类