题目内容
已知函数f(x)=ax(a>0且a≠1)
(1)若f(x0)=2,求f(3x0)的值;
(2)若f(x2-3x+1)≤f(x2+2x-4),求x的取值范围.
(1)若f(x0)=2,求f(3x0)的值;
(2)若f(x2-3x+1)≤f(x2+2x-4),求x的取值范围.
考点:函数单调性的性质,函数的值
专题:计算题
分析:(1)利用指数幂的运算性质,用f(x0)表示f(3x0);
(2)分0<a<1与a>1两种情况,利用函数的单调性求解不等式.
(2)分0<a<1与a>1两种情况,利用函数的单调性求解不等式.
解答:
解:(1)∵f(x)=ax,∴f(x0)=ax0=2,
∴f(3x0)=a3x0=(ax0)3=23=8,
(2)①当0<a<1时,
函数f(x)=ax在(-∞,+∞)上为减函数,
∴f(x2-3x+1)≤f(x2+2x-4)?x2-3x+1≥x2+2x-4,解得x≤1;
②当a>1时,
函数f(x)=ax在(-∞,+∞)上为增函数,
∴f(x2-3x+1)≤f(x2+2x-4)?x2-3x+1≤x2+2x-4,解得x≥1;
综上:①当0<a<1时,x∈(-∞,1];
②当a>1时,x∈[1,+∞).
∴f(3x0)=a3x0=(ax0)3=23=8,
(2)①当0<a<1时,
函数f(x)=ax在(-∞,+∞)上为减函数,
∴f(x2-3x+1)≤f(x2+2x-4)?x2-3x+1≥x2+2x-4,解得x≤1;
②当a>1时,
函数f(x)=ax在(-∞,+∞)上为增函数,
∴f(x2-3x+1)≤f(x2+2x-4)?x2-3x+1≤x2+2x-4,解得x≥1;
综上:①当0<a<1时,x∈(-∞,1];
②当a>1时,x∈[1,+∞).
点评:本题主要考查指数幂的运算性质,同时考查指数函数的性质,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
△ABC中,a=2,b=
,B=
,则sinA的值是( )
| 6 |
| π |
| 3 |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
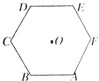 已知正六边形ABCDEF,边长为1,其中心为O.
已知正六边形ABCDEF,边长为1,其中心为O.