题目内容
已知函数f(x)=a1nx-ax-3(a≠0)
(1)讨论函数f(x)的单调性;
(2)若函数y=f(x)的图象在点(2,f(2))处的切线的倾斜角为45°,那么实数m在什么范围取值时,函数g(x)=x3+x2[
+f′(x)]在区间(2,3)内总存在极值?
(3)求证:
×
×
×
×
<
(n≥2,n∈N*).
(1)讨论函数f(x)的单调性;
(2)若函数y=f(x)的图象在点(2,f(2))处的切线的倾斜角为45°,那么实数m在什么范围取值时,函数g(x)=x3+x2[
| m |
| 2 |
(3)求证:
| 1n2 |
| 2 |
| 1n3 |
| 3 |
| 1n4 |
| 4 |
| 1n5 |
| 5 |
| 1nn |
| n |
| 1 |
| n |
考点:利用导数研究函数的单调性,利用导数研究函数的极值,利用导数求闭区间上函数的最值
专题:导数的综合应用
分析:(1)在求单调区间时要注意函数的定义域以及对参数a的讨论情况;
(2)点(2,f(2))处的切线的倾斜角为45°,即切线斜率为1,即f′(2)=1,可求a值,代入得g(x)的解析式,由t∈[1,2],且g(x)在区间(t,3)上总不是单调函数可知:g′(1)<0,g′(2)<0,g′(3)>0,于是可求m的范围.
(3)判断lnx<x-1对一切x∈(1,+∞)成立,进而可得0<
<
,即可证得结论.
(2)点(2,f(2))处的切线的倾斜角为45°,即切线斜率为1,即f′(2)=1,可求a值,代入得g(x)的解析式,由t∈[1,2],且g(x)在区间(t,3)上总不是单调函数可知:g′(1)<0,g′(2)<0,g′(3)>0,于是可求m的范围.
(3)判断lnx<x-1对一切x∈(1,+∞)成立,进而可得0<
| lnn |
| n |
| n-1 |
| n |
解答:
(1)解:f′(x)=
(x>0),
当a>0时,f(x)的单调增区间为(0,1],减区间为[1,+∞);
当a<0时,f(x)的单调增区间为[1,+∞),减区间为(0,1];
当a=0时,f(x)不是单调函数.
(2)解:f′(2)=-
=1得a=-2,f(x)=-2lnx+2x-3
∴g(x)=x3+(
+2)x2-2x,
∴g′(x)=3x2+(m+4)x-2
∵g(x)在区间(t,3)上总不是单调函数,且g′(0)=-2
∴g′(t)<0,g′(3)>0
由题意知:对于任意的t∈[1,2],g′(t)<0恒成立,
所以有
,∴存在-
<m<-9.
(3)证明:令a=-1此时f(x)=-lnx+x-3,所以f(1)=-2,
由(Ⅰ)知f(x)=-lnx+x-3在(1,+∞)上单调递增,
∴当x∈(1,+∞)时f(x)>f(1),即-lnx+x-1>0,
∴lnx<x-1对一切x∈(1,+∞)成立,(12分)
∵n≥2,n∈N*,则有0<lnn<n-1,
∴0<
<
,
∴
×
×…×
<
×
×
×…×
<
(n≥2,n∈N*).
| a(1-x) |
| x |
当a>0时,f(x)的单调增区间为(0,1],减区间为[1,+∞);
当a<0时,f(x)的单调增区间为[1,+∞),减区间为(0,1];
当a=0时,f(x)不是单调函数.
(2)解:f′(2)=-
| a |
| 2 |
∴g(x)=x3+(
| m |
| 2 |
∴g′(x)=3x2+(m+4)x-2
∵g(x)在区间(t,3)上总不是单调函数,且g′(0)=-2
∴g′(t)<0,g′(3)>0
由题意知:对于任意的t∈[1,2],g′(t)<0恒成立,
所以有
|
| 37 |
| 3 |
(3)证明:令a=-1此时f(x)=-lnx+x-3,所以f(1)=-2,
由(Ⅰ)知f(x)=-lnx+x-3在(1,+∞)上单调递增,
∴当x∈(1,+∞)时f(x)>f(1),即-lnx+x-1>0,
∴lnx<x-1对一切x∈(1,+∞)成立,(12分)
∵n≥2,n∈N*,则有0<lnn<n-1,
∴0<
| lnn |
| n |
| n-1 |
| n |
∴
| ln2 |
| 2 |
| ln3 |
| 3 |
| lnn |
| n |
| 1 |
| 2 |
| 2 |
| 3 |
| 3 |
| 4 |
| n-1 |
| n |
| 1 |
| n |
点评:本题考查利用函数的导数来求函数的单调区间,与函数结合证明不等式问题,常用的解题思路是利用前面的结论构造函数,利用函数的单调性,对于函数取单调区间上的正整数自变量n有某些结论成立,进而解答出这类不等式问题的解.

练习册系列答案
 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
函数f(x)=
,若函数g(x)=f(x)-kx+k的零点有2个,则k的取值范围( )
|
| A、(1,2] |
| B、(0,1] |
| C、(1,3] |
| D、(1,+∞) |
命题p:?x∈R,ax2+ax+1≥0,若?p是真命题,则实数a的取值范围是( )
| A、(0,4] |
| B、[0,4] |
| C、(-∞,0]∪[4,+∞) |
| D、(-∞,0)∪(4,+∞) |
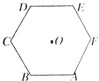 已知正六边形ABCDEF,边长为1,其中心为O.
已知正六边形ABCDEF,边长为1,其中心为O.