题目内容
已知二次函数f(x)的二次项系数为正且f(2-x)=f(2+x).求不等式f(2-
x2)<f(-x2+6x-7)的解集.
| 1 |
| 2 |
考点:二次函数的性质
专题:综合题,函数的性质及应用
分析:确定f(x)的对称轴为x=2,f(x)在(-∞,2]上是减函数,结合f(2-
x2)<f(-x2+6x-7),可得2-
x2>-x2+6x-7,即可求解集.
| 1 |
| 2 |
| 1 |
| 2 |
解答:
解:∵f(2-x)=f(2+x),∴f(x)的对称轴为x=2,
又∵f(x)的二次项系数大于零,∴f(x)在(-∞,2]上是减函数,
又∵2-
x2≤2,-x2+6x-7=-(x-3)2+2≤2,
∴2-
x2>-x2+6x-7,即x2-12x+18>0,
解得x<6-3
或x>6+3
.
故原不等式的解集为:{x|x>6+3
或x<6-3
}.
又∵f(x)的二次项系数大于零,∴f(x)在(-∞,2]上是减函数,
又∵2-
| 1 |
| 2 |
∴2-
| 1 |
| 2 |
解得x<6-3
| 2 |
| 2 |
故原不等式的解集为:{x|x>6+3
| 2 |
| 2 |
点评:本题考查二次函数的性质,考查函数的单调性,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
命题p:?x∈R,ax2+ax+1≥0,若?p是真命题,则实数a的取值范围是( )
| A、(0,4] |
| B、[0,4] |
| C、(-∞,0]∪[4,+∞) |
| D、(-∞,0)∪(4,+∞) |
已知函数f(x),g(x)分别由表给出:
则满足f(g(x))<g(f(x))的x的值为( )
| x | 1 | 2 | 3 |
| f(x) | 1 | 1 | 1 |
| x | 1 | 2 | 3 |
| g(x) | 3 | 2 | 1 |
| A、1 | B、2 |
| C、1或2 | D、1或2或3 |
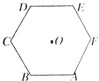 已知正六边形ABCDEF,边长为1,其中心为O.
已知正六边形ABCDEF,边长为1,其中心为O.