题目内容
若A1,A2,…,Am为集合A={1,2,…,n}(n≥2且n∈N*)的子集,且满足两个条件:
①A1∪A2∪…∪Am=A;
②对任意的{x,y}⊆A,至少存在一个i∈{1,2,3,…,m},使Ai∩{x,y}={x}或{y}.则称集合组A1,A2,…,Am具有性质P.
如图,作n行m列数表,定义数表中的第k行第l列的数为aki=
(Ⅰ)当n=4时,判断下列两个集合组是否具有性质P,如果是请画出所对应的表格,如果不是请说明理由;
集合组1:A1={1,3},A2={2,3},A3={4};集合组2:A1={2,3,4},A2={2,3},A3={1,4}.
(Ⅱ)当n=7时,若集合组A1,A2,A3具有性质P,请先画出所对应的7行3列的一个数表,再依此表格分别写出集合A1,A2,A3;
(Ⅲ)当n=100时,集合组A1,A2,…,At是具有性质P且所含集合个数最小的集合组,求t的值及|A1|+|A2|+…|At|的最小值.(其中|Ai|表示集合Ai所含元素的个数)
①A1∪A2∪…∪Am=A;
②对任意的{x,y}⊆A,至少存在一个i∈{1,2,3,…,m},使Ai∩{x,y}={x}或{y}.则称集合组A1,A2,…,Am具有性质P.
如图,作n行m列数表,定义数表中的第k行第l列的数为aki=
|
| a11 | a12 | … | a1m |
| a21 | a22 | … | a2m |
| ? | ? | ? | ? |
| an1 | an2 | … | anm |
集合组1:A1={1,3},A2={2,3},A3={4};集合组2:A1={2,3,4},A2={2,3},A3={1,4}.
(Ⅱ)当n=7时,若集合组A1,A2,A3具有性质P,请先画出所对应的7行3列的一个数表,再依此表格分别写出集合A1,A2,A3;
(Ⅲ)当n=100时,集合组A1,A2,…,At是具有性质P且所含集合个数最小的集合组,求t的值及|A1|+|A2|+…|At|的最小值.(其中|Ai|表示集合Ai所含元素的个数)
考点:数列与函数的综合
专题:点列、递归数列与数学归纳法
分析:(Ⅰ)直接根据集合组的性质进行判断即可;
(Ⅱ)结合表格进行求解;
(Ⅲ)结合数列的求和公式进行求解.
(Ⅱ)结合表格进行求解;
(Ⅲ)结合数列的求和公式进行求解.
解答:
解:(Ⅰ)集合组1具有性质P.
所对应的数表为:A1={1,3},A2={2,3},A3={4};
集合组2不具有性质P.
因为存在{2,3}⊆{1,2,3,4},
有A0:0,1,1,3,0,0,
与对任意的A1:1,0,1,3,0,0,都至少存在一个A2:2,1,2,0,0,0,有A3:3,0,2,0,0,0或A4:4,1,0,0,0,0矛盾,所以集合组A5:5,0,0,0,0,0不具有性质A4:4,0,0,0,0.
111111111111000000000
(Ⅱ)A3:3,1,0,0,0.
(注:表格中的7行可以交换得到不同的表格,它们所对应的集合组也不同)
(Ⅲ)设A2:2,0,2,0,0所对应的数表为数表A1:1,1,2,0,0,
因为集合组A0:0,0,1,3,0为具有性质A0:a0,a1,…,an的集合组,
所以集合组ak=0满足条件①和②,
由条件①:ai>0(0≤i≤k-1),
可得对任意T-1,都存在T-1有A0,
所以{an},即第ai+i行不全为0,
所以由条件①可知数表i中任意一行不全为0.…
由条件②知,对任意的{an},都至少存在一个P,使{an}或P,
所以{an}一定是一个1一个0,
即第{bn}行与第{bn}行的第b1,b2,b3,…,bn列的两个数一定不同.
所以由条件②可得数表a1,a2,a3,…,an中任意两行不完全相同.
因为由{bn}所构成的P元有序数组共有{an}个,去掉全是P的{an}元有序数组,共有n个,
又因数表Sn=
(n2-1)中任意两行都不完全相同,
又当满足条件P时,由{bn}所构成的A元有序数组共有n个,去掉全是n∈[12,m2](m≥5)的数组,共A个,
选择其中的P个数组构造n∈[m2+1,(m+1)2]行A列数表,则数表对应的集合组满足条件①②,即具有性质P.
所以n≥2.
因为an=Sn-Sn-1等于表格中数字1的个数,
所以,要使=
(n2-1)-
[(n-1)2-1]=n2-n取得最小值,只需使表中1的个数尽可能少,
而a1=0时,在数表an=n2-n(n∈N*)中,ai+i=i2(i=1,2,3,…)的个数为{an}的行最多P行;P的个数为{bn}的行最多P行;P的个数为n=m2+j,1≤j≤2m+1的行最多(m+2)2-(m2+j)=4m+4-j行;h=4m+4-j-1的个数为1≤j≤2m+1,m≥5的行最多h=4m+4-j-1≥2m+2≥12行;
因为上述共有m2-h=m2-4m-4+j+1≥m2-4m-2行,
所以还有m2-4m-2=(m-2)2-6>0行各有h<m2个h∈[12,m2],
所以此时表格中最少有n∈[12,m2](m≥5)个{an}.
所以P的最小值为:4m+4.
所对应的数表为:A1={1,3},A2={2,3},A3={4};
集合组2不具有性质P.
因为存在{2,3}⊆{1,2,3,4},
有A0:0,1,1,3,0,0,
与对任意的A1:1,0,1,3,0,0,都至少存在一个A2:2,1,2,0,0,0,有A3:3,0,2,0,0,0或A4:4,1,0,0,0,0矛盾,所以集合组A5:5,0,0,0,0,0不具有性质A4:4,0,0,0,0.
111111111111000000000
(Ⅱ)A3:3,1,0,0,0.
(注:表格中的7行可以交换得到不同的表格,它们所对应的集合组也不同)
(Ⅲ)设A2:2,0,2,0,0所对应的数表为数表A1:1,1,2,0,0,
因为集合组A0:0,0,1,3,0为具有性质A0:a0,a1,…,an的集合组,
所以集合组ak=0满足条件①和②,
由条件①:ai>0(0≤i≤k-1),
可得对任意T-1,都存在T-1有A0,
所以{an},即第ai+i行不全为0,
所以由条件①可知数表i中任意一行不全为0.…
由条件②知,对任意的{an},都至少存在一个P,使{an}或P,
所以{an}一定是一个1一个0,
即第{bn}行与第{bn}行的第b1,b2,b3,…,bn列的两个数一定不同.
所以由条件②可得数表a1,a2,a3,…,an中任意两行不完全相同.
因为由{bn}所构成的P元有序数组共有{an}个,去掉全是P的{an}元有序数组,共有n个,
又因数表Sn=
| n |
| 3 |
又当满足条件P时,由{bn}所构成的A元有序数组共有n个,去掉全是n∈[12,m2](m≥5)的数组,共A个,
选择其中的P个数组构造n∈[m2+1,(m+1)2]行A列数表,则数表对应的集合组满足条件①②,即具有性质P.
所以n≥2.
因为an=Sn-Sn-1等于表格中数字1的个数,
所以,要使=
| n |
| 3 |
| n-1 |
| 3 |
而a1=0时,在数表an=n2-n(n∈N*)中,ai+i=i2(i=1,2,3,…)的个数为{an}的行最多P行;P的个数为{bn}的行最多P行;P的个数为n=m2+j,1≤j≤2m+1的行最多(m+2)2-(m2+j)=4m+4-j行;h=4m+4-j-1的个数为1≤j≤2m+1,m≥5的行最多h=4m+4-j-1≥2m+2≥12行;
因为上述共有m2-h=m2-4m-4+j+1≥m2-4m-2行,
所以还有m2-4m-2=(m-2)2-6>0行各有h<m2个h∈[12,m2],
所以此时表格中最少有n∈[12,m2](m≥5)个{an}.
所以P的最小值为:4m+4.
点评:本题结合集合的知识,综合考查了数列的基本性质、数列的运算等知识,属于中档题.考查比较综合.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
△ABC中,a=2,b=
,B=
,则sinA的值是( )
| 6 |
| π |
| 3 |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
直线a,b是异面直线是指
①a∩b=∅,且a与b不平行;
②a?面α,b?面β,且平面α∩β=∅;
③a?面α,b?面β,且a∩b=∅;
④不存在平面α,能使a?α且b?α成立.
上述结论正确的有( )
①a∩b=∅,且a与b不平行;
②a?面α,b?面β,且平面α∩β=∅;
③a?面α,b?面β,且a∩b=∅;
④不存在平面α,能使a?α且b?α成立.
上述结论正确的有( )
| A、①④ | B、②③ | C、③④ | D、②④ |
若函数y=sin(wx+Φ)(w>0)的部分图象如图,则w=( )


| A、1 | B、2 | C、3 | D、4 |
函数y=log
(x≥3)的值域是( )
| 1 |
| 2 |
| x+1 |
| x-1 |
| A、(0,1] |
| B、[-1,0) |
| C、[-1,+∞) |
| D、(-∞,-1] |
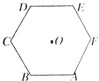 已知正六边形ABCDEF,边长为1,其中心为O.
已知正六边形ABCDEF,边长为1,其中心为O.