题目内容
从原点向圆x2+y2-12y+27=0作两条切线,则这两个切点之间的距离为 .
考点:圆的切线方程
专题:直线与圆
分析:首先把圆的一般方程转化为标准方程,进一步得到三角形相似,利用勾股定理进一步求的结果.
解答:

解:过O向圆引切线OM,连结AM,得AM⊥OM,
∵x2+y2-12y+27=0,
∴x2+(y-6)2=9,
即OA=6,AM=3,
根据△AMN∽△AOM,
AM2=AN•AO,
求得AN=
,
在△ANM中利用勾股定理求得:MN=
,
两切点间的距离为:3
.
故答案为:3
.

解:过O向圆引切线OM,连结AM,得AM⊥OM,
∵x2+y2-12y+27=0,
∴x2+(y-6)2=9,
即OA=6,AM=3,
根据△AMN∽△AOM,
AM2=AN•AO,
求得AN=
| 3 |
| 2 |
在△ANM中利用勾股定理求得:MN=
3
| ||
| 2 |
两切点间的距离为:3
| 3 |
故答案为:3
| 3 |
点评:本题考查的知识点:圆的一般方程与标准方程之间的转化,三角形的相似,勾股定理及相关的运算问题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
函数f(x)=
,若函数g(x)=f(x)-kx+k的零点有2个,则k的取值范围( )
|
| A、(1,2] |
| B、(0,1] |
| C、(1,3] |
| D、(1,+∞) |
命题p:?x∈R,ax2+ax+1≥0,若?p是真命题,则实数a的取值范围是( )
| A、(0,4] |
| B、[0,4] |
| C、(-∞,0]∪[4,+∞) |
| D、(-∞,0)∪(4,+∞) |
△ABC中,a=2,b=
,B=
,则sinA的值是( )
| 6 |
| π |
| 3 |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
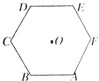 已知正六边形ABCDEF,边长为1,其中心为O.
已知正六边形ABCDEF,边长为1,其中心为O.