题目内容
已知a，b为正数，则“a+b≤2“是“
+
≤2“成立的（ ）
| a |
| b |
| A、充分非必要条件 |
| B、必要非充分条件 |
| C、充分必要条件 |
| D、既非充分也非必要条件 |
考点：必要条件、充分条件与充要条件的判断
专题：简易逻辑
分析：根据充分条件和必要条件的定义进行判断即可．
解答：
解：若a+b≤2，
则（
+
）2=a+b+2
•
≤a+b+a+b=2（a+b）≤4，
即
+
≤2成立，即充分性成立，
设x=
，y=
，则a=x2，b=y2，
则不等式a+b≤2等价为x2+y2≤2，
+
≤2等价为x+y≤2，
则由图象可知必要性成立，
故“a+b≤2“是“
+
≤2“成立充要条件，
故选：C
则（
| a |
| b |
| a |
| b |
即
| a |
| b |
设x=
| a |
| b |
则不等式a+b≤2等价为x2+y2≤2，
| a |
| b |
则由图象可知必要性成立，
故“a+b≤2“是“
| a |
| b |
故选：C
点评：本题主要考查充分条件和必要条件的判断，比较基础．
练习册系列答案
相关题目
下列函数中，不具有奇偶性的是（ ）
| A、y=x2-1 | ||||
| B、y=sinxcosx | ||||
C、y=
| ||||
| D、y=lgx2 |
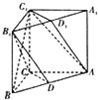直三棱柱ABC-A1B1C1中，AC=CC1=BC=1，∠BCA=90°，D、D1分别是AB与A1B1的中点．