题目内容
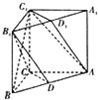 直三棱柱ABC-A1B1C1中,AC=CC1=BC=1,∠BCA=90°,D、D1分别是AB与A1B1的中点.
直三棱柱ABC-A1B1C1中,AC=CC1=BC=1,∠BCA=90°,D、D1分别是AB与A1B1的中点.(1)求异面直线AC1与A1B1所成的角的大小;
(2)求证:平面AC1D1∥平面B1CD.
考点:平面与平面平行的判定,异面直线及其所成的角
专题:证明题,空间位置关系与距离
分析:(1)根据已知可得AB=
,AC1=
,BC1=
,从而可求∠C1AB=
,由A1B1∥AB,可得异面直线AC1与A1B1所成的角=∠C1AB=
.
(2)先证明AD1
DB1再证明,C1D1
CD,由于AD1∩C1D1=D1,CD∩DB1=D,从而可证平面AC1D1∥平面B1CD.
| 2 |
| 2 |
| 2 |
| π |
| 3 |
| π |
| 3 |
(2)先证明AD1
| ∥ |
. |
| ∥ |
. |
解答:
解:(1)∵直三棱柱ABC-A1B1C1中,AC=CC1=BC=1,∠BCA=90°
∴AB=
=
,AC1=
=
,BC1=
=
∴△ABC1是正三角形,∠C1AB=
,
∵A1B1∥AB
∴异面直线AC1与A1B1所成的角=∠C1AB=
.
(2)证明:∵直三棱柱ABC-A1B1C1中,B1D1
AD,
∴AD1
DB1
∵直三棱柱ABC-A1B1C1中,C1D1
CD
又∵AD1∩C1D1=D1,CD∩DB1=D
∴平面AC1D1∥平面B1CD.
∴AB=
| BC2+AC2 |
| 2 |
| AC2+CC21 |
| 2 |
| BC2+CC12 |
| 2 |
∴△ABC1是正三角形,∠C1AB=
| π |
| 3 |
∵A1B1∥AB
∴异面直线AC1与A1B1所成的角=∠C1AB=
| π |
| 3 |
(2)证明:∵直三棱柱ABC-A1B1C1中,B1D1
| ∥ |
. |
∴AD1
| ∥ |
. |
∵直三棱柱ABC-A1B1C1中,C1D1
| ∥ |
. |
又∵AD1∩C1D1=D1,CD∩DB1=D
∴平面AC1D1∥平面B1CD.
点评:本题主要考查了平面与平面平行的判定,异面直线及其所成的角的解法,属于基本知识的考查.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案
相关题目
已知a,b为正数,则“a+b≤2“是“
+
≤2“成立的( )
| a |
| b |
| A、充分非必要条件 |
| B、必要非充分条件 |
| C、充分必要条件 |
| D、既非充分也非必要条件 |
已知正方形ABCD的边长为2,P为其外接圆上一动点,则
•
的最大值为( )
| AB |
| AP |
A、2+2
| ||
B、2+
| ||
C、2+2
| ||
D、2+
|
已知f(n)=
若 an=f(n)+f(n+1),则a1+a2+…+a2014=( )
|
| A、-1 | B、2012 |
| C、0 | D、-2012 |
已知等差数列{an}中,有
+1<0,且它们的前n项和Sn有最大值,则使得Sn>0的n的最大值为( )
| a2014 |
| a2013 |
| A、4024 | B、4025 |
| C、4026 | D、4027 |