题目内容
设函数f(x)=
x2-(a+b)x+ablnx(其中e为自然对数的底数,a≠e,b∈R),曲线y=f(x)在点(e,f(e))处的切线方程为y=-
e2.
(1)求b;
(2)若对任意x∈[
,+∞),f(x)有且只有两个零点,求a的取值范围.
| 1 |
| 2 |
| 1 |
| 2 |
(1)求b;
(2)若对任意x∈[
| 1 |
| e |
考点:利用导数研究曲线上某点切线方程,函数零点的判定定理
专题:计算题,函数的性质及应用,导数的概念及应用,导数的综合应用
分析:(1)求导f′(x)=x-(a+b)+
=
,从而求b;
(2)由(1)得f(x)=
x2-(a+e)x+aelnx,f′(x)=
,从而①当a≤
时,要使得f(x)在[
,+∞)上有且只有两个零点,只需f(
)=
-
+aeln
=
≥0,②当
<a<e时,求导确定零点个数,③当a>e时,求导确定零点个数.
| ab |
| x |
| (x-a)(x-b) |
| x |
(2)由(1)得f(x)=
| 1 |
| 2 |
| (x-a)(x-e) |
| x |
| 1 |
| e |
| 1 |
| e |
| 1 |
| e |
| 1 |
| 2e2 |
| a+e |
| e |
| 1 |
| e |
| (1-2e2)-2e(1+e2)a |
| 2e2 |
| 1 |
| e |
解答:
解:(1)f′(x)=x-(a+b)+
=
,
∵f′(e)=0,a≠e,
∴b=e;
(2)由(1)得f(x)=
x2-(a+e)x+aelnx,f′(x)=
,
①当a≤
时,由f′(x)>0得x>e;由f′(x)<0得
<x<e.
此时f(x)在(
,e)上单调递减,在(e,+∞)上单调递增.
∵f(e)=
e2-(a+e)e+aelne=-
e2<0,
f(e2)=
e4-(a+e)e2+2ae=
e(e-2)(e2-2a)≥
e(e-2)(e2-
)>0;
∴要使得f(x)在[
,+∞)上有且只有两个零点,
则只需f(
)=
-
+aeln
=
≥0,
即a≤
;
②当
<a<e时,
由f′(x)>0得
<x<a或x>e;由f′(x)<0得a<x<e.
此时f(x)在(a,e)上单调递减,在(
,a)和(e,+∞)上单调递增.
此时f(a)=-
a2-ae+aelna<-
a2-ae+aelne=-
a2<0,
∴此时f(x)在[e,+∞)至多只有一个零点,不合题意;
③当a>e时,
由f′(x)>0得
<x<e或x>a,由f′(x)<0得e<x<a,
此时f(x)在(
,e)和(a,+∞)上单调递增,在(e,a)上单调递减,且f(e)=-
e2<0,
∴f(x)在[
,+∞)至多只有一个零点,不合题意.
综上所述,a的取值范围为(-∞,
].
| ab |
| x |
| (x-a)(x-b) |
| x |
∵f′(e)=0,a≠e,
∴b=e;
(2)由(1)得f(x)=
| 1 |
| 2 |
| (x-a)(x-e) |
| x |
①当a≤
| 1 |
| e |
| 1 |
| e |
此时f(x)在(
| 1 |
| e |
∵f(e)=
| 1 |
| 2 |
| 1 |
| 2 |
f(e2)=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| e |
∴要使得f(x)在[
| 1 |
| e |
则只需f(
| 1 |
| e |
| 1 |
| 2e2 |
| a+e |
| e |
| 1 |
| e |
| (1-2e2)-2e(1+e2)a |
| 2e2 |
即a≤
| 1-2e2 |
| 2e(1+e2) |
②当
| 1 |
| e |
由f′(x)>0得
| 1 |
| e |
此时f(x)在(a,e)上单调递减,在(
| 1 |
| e |
此时f(a)=-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴此时f(x)在[e,+∞)至多只有一个零点,不合题意;
③当a>e时,
由f′(x)>0得
| 1 |
| e |
此时f(x)在(
| 1 |
| e |
| 1 |
| 2 |
∴f(x)在[
| 1 |
| e |
综上所述,a的取值范围为(-∞,
| 1-2e2 |
| 2e(1+e2) |
点评:本题考查了导数的综合应用及导数的几何意义的应用,同时考查了分类讨论的思想应用,属于中档题.

练习册系列答案
相关题目
下列四组函数,表示同一函数的是( )
A、f(x)=
| ||||||
B、f(x)=x,g(x)=
| ||||||
C、f(x)=
| ||||||
D、f(x)=x,g(x)=
|
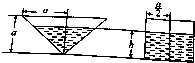 一个圆锥形容器和一个圆柱形容器的轴截面的尺寸如图,两容器盛有液体的体积正好相等,且液面高均为h,求h.
一个圆锥形容器和一个圆柱形容器的轴截面的尺寸如图,两容器盛有液体的体积正好相等,且液面高均为h,求h.