Question

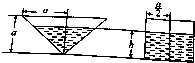一个圆锥形容器和一个圆柱形容器的轴截面的尺寸如图，两容器盛有液体的体积正好相等，且液面高均为h，求h．

Answer 1

考点：旋转体（圆柱、圆锥、圆台）

专题：空间位置关系与距离

分析：根据已知中圆锥形容器和圆柱形容器的轴截面的尺寸，计算出液体的体积，结合两容器盛有液体的体积正好相等，且液面高均为h，构造关于h的方程，解得答案．

解答： 解：∵圆锥的底面半径为a时，高为h，
故液面高为h时，底面半径为h，
故圆锥体内液体的体积为：

1

3

πh2•h=

1

3

πh3，
又∵圆柱的底面半径为

a

2

，液面高为h，
故圆柱体内液体的体积为：π•(

a

2

)2•h=

1

4

πa2h，
由两容器盛有液体的体积正好相等，
∴

1

3

πh3=

1

4

πa2h，
解得：h=

3

2

a

点评：本题考查的知识点是旋转体，熟练掌握圆锥和圆柱的体积公式，是解答的关键．