题目内容
已知圆锥的轴截面是边长为2的正三角形，则该圆锥的体积为 ．
考点：旋转体（圆柱、圆锥、圆台）
专题：空间位置关系与距离
分析：根据圆角轴截面的定义结合正三角形的性质，可得圆锥底面半径长和高的大小，由此结合圆锥的体积公式，则不难得到本题的答案．
解答：
解：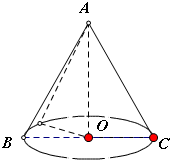
∵圆锥的轴截面是正三角形ABC，边长等于2
∴圆锥的高AO=
×2=
，
底面半径r=
×2=1
因此，该圆锥的体积V=
πr2•AO=
π×12×
=
π
故答案为：
π；
∵圆锥的轴截面是正三角形ABC，边长等于2∴圆锥的高AO=
| ||
| 2 |
| 3 |
底面半径r=
| 1 |
| 2 |
因此，该圆锥的体积V=
| 1 |
| 3 |
| 1 |
| 3 |
| 3 |
| ||
| 3 |
故答案为：
| ||
| 3 |
点评：本题给出圆锥轴截面的形状，求圆锥的体积，着重考查了等边三角形的性质和圆锥的轴截面等知识，属于基础题．
练习册系列答案
相关题目
已知某几何体的三视图如图所示，则该几何体的体积为（ ）
| A、4 | ||
B、
| ||
| C、8 | ||
D、
|
将正整数按下表的规律排列，把行与列交叉处的一个数称为某行某列的数，记作aij（i，j∈N*），如第2行第4列的数是15，记作a24=15，则a82是若正项数列{an}满足lgan+1=1+lgan，且a2001+a2002+…+a2010=2014，则a2011+a2012+…+a2020的值为（ ）
| A、2014•1010 |
| B、2014•1011 |
| C、2015•1010 |
| D、2015•1011 |