题目内容
已知函数f(x)=
,若方程|f(x)|=a有三个零点,则实数a的取值范围是 .
|
考点:函数零点的判定定理
专题:计算题,函数的性质及应用
分析:由题意可知a≥0,分类讨论方程|f(x)|=a的根即可.
解答:
解:∵方程|f(x)|=a有三个根,
∴a≥0,
若a=0,则方程|f(x)|=a只有一个根,故不成立;
若a>0,
∵当x<1时,f(x)=3x∈(0,3)
当x≥1时,f(x)=3-log3x≤3,且单调,
则若方程|f(x)|=a有三个根,则在x<1有一个,
在x≥1时有两个,
则实数a的取值范围是(0,3).
故答案为(0,3).
∴a≥0,
若a=0,则方程|f(x)|=a只有一个根,故不成立;
若a>0,
∵当x<1时,f(x)=3x∈(0,3)
当x≥1时,f(x)=3-log3x≤3,且单调,
则若方程|f(x)|=a有三个根,则在x<1有一个,
在x≥1时有两个,
则实数a的取值范围是(0,3).
故答案为(0,3).
点评:本题考查了方程的根与函数的零点之间的关系,属于基础题.

练习册系列答案
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
有穷数列5,8,11,…3n+11(n∈N*)的项数是( )
| A、n | B、3n+11 |
| C、n+4 | D、n+3 |
等比数列{an}中,S2=7,S6=91,则S4=( )
| A、28或-21 | B、28 |
| C、-21 | D、以上都不对 |
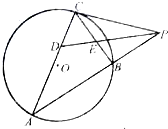 如图,PC是圆O的切线,切点为C,直线PA与圆O交于两点A、B,∠APC的平分线分别交弦CA、CB于两点D、E,已知PC=3,PB=2,则
如图,PC是圆O的切线,切点为C,直线PA与圆O交于两点A、B,∠APC的平分线分别交弦CA、CB于两点D、E,已知PC=3,PB=2,则